はじめにたまっていた仕事量、新たに入ってくる仕事量がわかっている問題です。
浅野中学校合格のための過去問対策
浅野中学校・高等学校過去問対策
難関中学受験指導はスペースONEのプロ家庭教師にお任せください。
浅野中学校2007年度算数入試問題 3.ニュートン算 問題
A中学校では、入学願書の受付を午前９時に開始します。
ところが、開始するまでにすでに５５０人が受付の順番を待っていて、その後も毎分１０人の割合で人が到着してきます。
窓口を３つにして受付を開始すると、５０分で受付の順番を待つ人がいなくなります。
このとき次の問題に答えなさい。ただし、どの窓口でも、１人の受付に要する時間は同じ基します。(考え方と計算も書くこと）
このとき次の問題に答えなさい。ただし、どの窓口でも、１人の受付に要する時間は同じ基します。(考え方と計算も書くこと）
(1) １つの窓口で、１分間に受付のできる人数を求めなさい。
(2) 窓口を５つにして受付を開始すると、何分で受け絵付けの順番を待つ人がいなくなりますか。
(3) 受付を開始してから１０分以内に順番を待つ人がいなくなるようにするためには、受付窓口を最低何箇所にすればよいですか。
浅野中学校2007年度 算数入試問題 3.ニュートン算 (1) 解説解答
解説
開始前に受付の順番を待っている人が550人、毎分10人の割合で到着してくるので50分間では500人。
合わせて1050人を3つの窓口が50分間で受け付けます。
これをニュートン算の線分図で表しましょう。
１つの窓口が１分間に受け付ける人数を①にすると、
１つの窓口が１分間に受け付ける人数を①にすると、
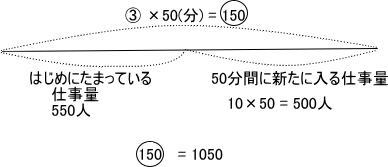
よって ① = 1050 ÷150 = 7
答 ７人
浅野中学校2007年度 算数入試問題 3.ニュートン算 (2) 解説解答
解説
（１）より ひとつの窓口で受け付ける人数は、１分間に７人です。
５つの窓口では１分間に７×５＝３５人ずつ受け付けますが、新たに１分間に１０人ずつ繰るので、１分当たりに減る行列の人数は３５－１０＝２５人です。
よって、９時前に待っていた人数がなくなるのは、５５０÷２５＝２２
答 ９時２２分
浅野中学校2007年度算数入試問題 3.ニュートン算 (3) 解説解答
解説
開始前に５５０人並んでいて その後も毎分１０人の割合で人が到着するので、１０分間に受け付ける人数の合計は
５５０＋１０×＝６５０(人）
この人数を１０分間で受け付けるとよいので、１分間では ６５０÷１０＝６５
１つの窓口では１分間に７人ずつ受け付けるので ６５÷７＝９.１・・・
答 １０