浅野中学校・浅野高等学校過去問研究
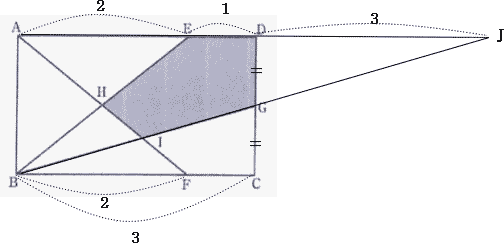
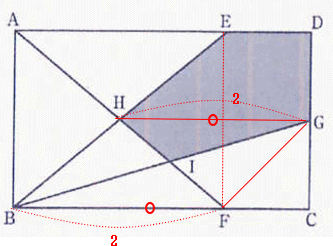
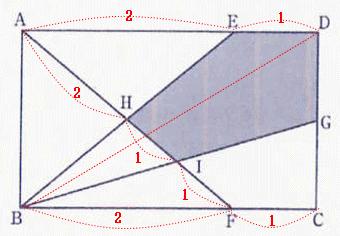
2017年度浅野中学校算数入試問題は例年通り大問６題構成でした。 出題内容は １．四則計算1問 ２．小問集合5問 ３．旅人算とグラフ ４．平面図形（円の性質と相似形） ５．整数の性質と約束記号 ６．立体図形でした。
試験時間は50分、配点120点 合格者平均得点率 60.1%、受験者平均得点率 49.9%でした。
今回は2．小問集合5問を解説します。
浅野中学校合格のための過去問対策
浅野中学校・高等学校過去問対策
難関中学受験指導はスペースONEのプロ家庭教師にお任せください。
浅野中学校2017年度算数入試問題 2.小問集合 問題
浅野中学校2017年度 算数入試問題 2.小問集合 (1) 倍数変化算 解説解答
解説解答
兄弟の残った金額が同じだったら、8と7の最小公倍数の56にするために、兄の線分図を7倍，弟の線分図を8倍にすると
⑨ = 1500 - 6000 = 4500円
はじめに兄が持っていた金額と弟が持っていた金額は
兄： 4500 ÷ 9 × 7 = 3500円
弟： 4500 ÷ 9 × 5 = 2500円
答 兄： 3500円 弟： 2500円
浅野中学校2017年度 算数入試問題 2.小問集合 (2) 旅人算 解説解答
1日目は A君が1周、B君が1周します。
2日目は A君が1周、B君が2周します。
3日目は A君が2周、B君が1周します。
4日目は A君が1周、B君が3周します。
5日目は A君が2周、B君が2周します。
6日目は A君が3周、B君が1周します。
7日目は A君が1周、B君が4周します。・・・
このとき、100日目は、A君は[(ウ)]周、B君は[(エ)]周します。
解説
A君は 1 / 1,2 / 1,2,3 / 1,2,3,4 /・・・
B君は 1/ 2,1 / 3,2,1 / 4,3,2,1/ ・・・の規則に従って走っているので、
A君は ( 1 + 13 ) ×13÷2 = 91 より A君は13周走った後、1,2,3・・・14周走るので、
100 - 91 = 9 ・・・A君は100日目は9周走り
14 - 9 + 1 = 6・・・B君は6周走る。
答 ウ： 9 エ： 6
浅野中学校2017年度 算数入試問題 2.小問集合 (3) 暦 解説解答
解説
Ａ君は3日ごとに、Ｂ君は5日ごとに通っているので、２人は3と5の最小公倍数15日ごとにこの図書館で出会う。
この次に２人が出会う最初の日は2017年4月30日
日曜日から15日後なので、15÷7 = 2・・・1 .
よって 日曜日の1日後 月曜日 ・・・[(オ)]
1週間は7日なので、この次に２人が出会う最初の日曜日は7と15の最小公倍数の105日後。
5月・・・31日，6月・・・30日，7月・・・31日なので、7月31日までに92日。
したがって 8月1日から 105 - 92 = 13日後 8月13日
答 オ：月，カ：8， キ:13
浅野中学校2017年度 算数入試問題 2.小問集合 (4) 差集め算 解説解答
解説
どら焼き2個とようかん4個と箱代で1150円
どら焼き6個とようかん2個と箱代で1250円 なので
どら焼き4個とようかん3個と箱代で1200円
どら焼き4個とようかん5個と箱代で1620円 なので、ようかん2個で420円 ようかん1個で420÷2 = 210円
どら焼き2個とようかん4個と箱代で1150円なので どら焼き2個と箱代で1150 - 210×4 = 310円
どら焼き6個とようかん2個と箱代で1250円なので どら焼き6個と箱代で1250円 - 210×2 = 830円
よって どら焼き1個で (830 - 310)÷4 = 130円
どら焼き2個とようかん4個と箱代で1150円なので、箱代は 1150 - 130×2 - 210×4 = 50円
どら焼きとようかんを3個，3個、にすると (130 + 210)×3 + 50 = 1070円
答 ク：50 ケ：1070
浅野中学校2017年度 算数入試問題 2.小問集合 (5) 平面図形 解説解答
コサ解説
図の通り辺ADと直線BGの延長線の交点をJとする。
三角形DGJと三角形CGBは相似形なので、DG：GC = DJ：BC = 1：1
三角形AIJと三角形FIBは相似形なのでBI：IJ = 2：6 = 1：3
BJの長さを1とすると
よって BI：IG = 1：1答 コ：1，サ：1，
コサ別解
図の通り点Hと点G，点Eと点F，点Fと点Gをそれぞれ直線で結ぶ。
四角形AEFBは長方形なので、対角線AF，BEの交点Hは対角線の中点なので、直線HGとBFは平行であり、HG = BF
よって四角形HBFGは平行四辺形。
したがって平行四辺形の対角線の交点は対角線の中点なので、BI = IG より BI：IG = 1：1
答 コ：1，サ：1，
長方形ABCDの面積が180c㎡のとき、色の付いている部分の五角形DEHIGの面積は[(シ)]c㎡になります。
シ解説
五角形DEHIGの面積 = 長方形ABCDの面積 - (三角形ABFの面積 + 三角形BHIの面積 + 三角形BGC面積)
