中学受験指導はスペースONEのプロ家庭教師にお任せください。
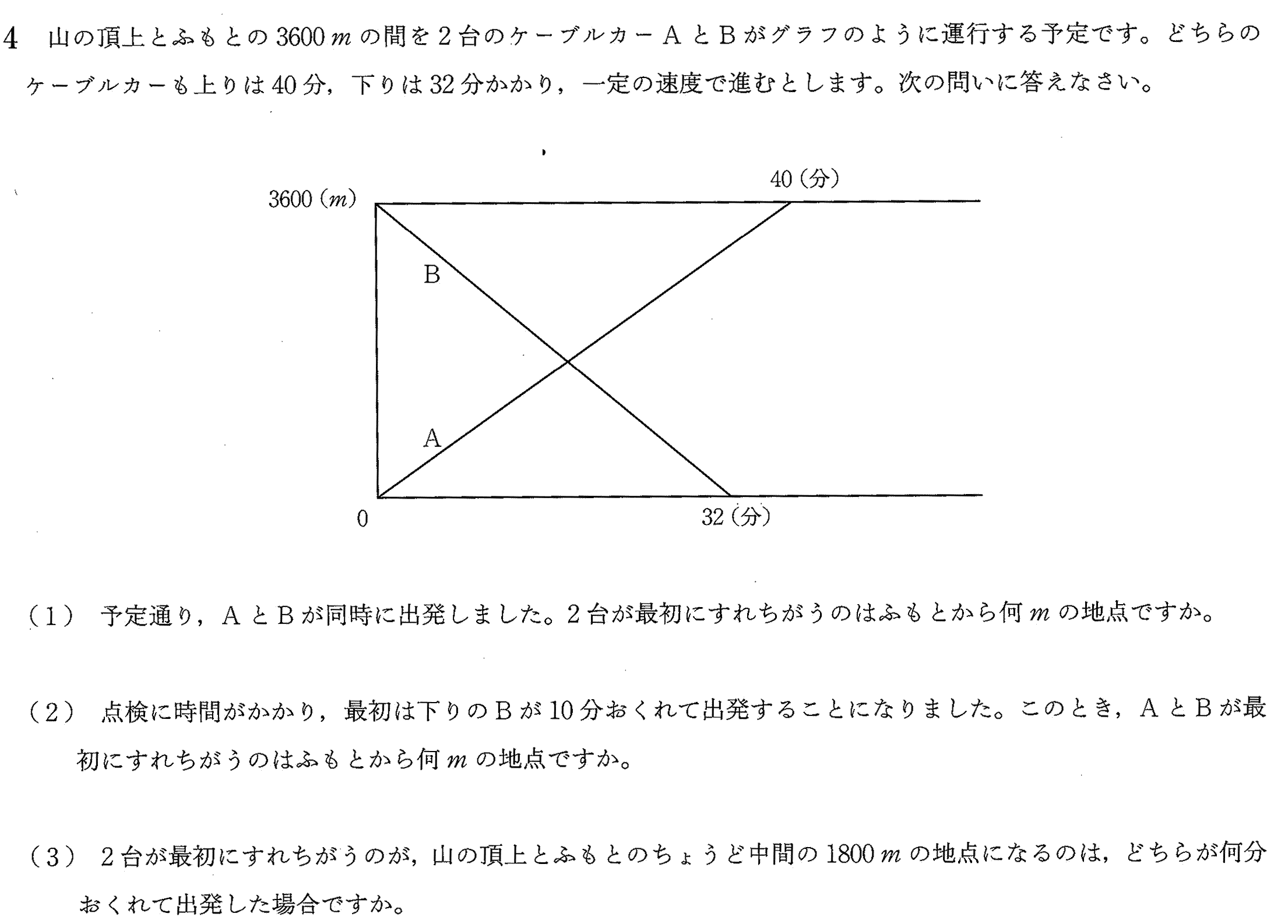
2014年度跡見学園中学校第１回算数入試問題は例年通りの出題構成で、１．計算４問 ２．小問集合６問 ３．４大問で、３．では規則性 ４．では旅人算（出会い算）でした。
受験者平均点 59.4点，合格者平均点 68.9点でした。難問はありませんので、特殊算の基本的な解き方を繰り返し練習しましょう。
算数入試問題（旅人算にチャレンジ）
算数は試験時間50分で総解答箇所16なので、スピードが要求されます。１．２は途中式を書かず答えのみを解答欄に書く解答形式ですが、３．４．は途中の考え方や式を書く解答形式です。要領よく式や考えをまとめる練習も必要です。
| (1) 予定通り、ＡとＢが同時に出発しました。２台が最初にすれちがうのはふもとから何ｍの地点ですか。 |
| 解説解答：比で求める |
| 上りと下りの時間の比は ４０：３２＝５：４ |
| よって 同じ時間に進む上りと下りの距離の比は ４：５ |
| ＡはふもとからＢは頂上から同時に進むので、Ａが進む距離がふもとからの距離になる。 |
| ３６００÷（５＋４）×４＝１６００ |
| 別解：速さの出会いで求める。 |
| 上りは４０分、下りは３２分かかるので、上りの速さは ３６００÷４０＝９０（ｍ/分） 下りの速さは ３６００÷３２＝１１２．５（ｍ/分） |
| よって ＡとＢが同時に出発して最初にすれちがうのは 出発して ｛３６００÷（９０＋１１２．５）｝分後なので、 |
| Ａが分速９０ｍで出発して｛３６００÷（９０＋１１２．５）｝分間進んだ地点 ３６００÷２０２．５×９０＝１６００ |
| 答 １６００ｍ |
| (2) 点検に時間がかかり、、最初は下りのＢが１０分おくれて出発することになりました。このとき、ＡとＢが最初にすれ違うのはふもとから何ｍの地点ですか。 |
| 解説解答：速さの出会いで求める。 |
| 上りは４０分、下りは３２分かかるので、上りの速さは ３６００÷４０＝９０（ｍ/分） 下りの速さは ３６００÷３２＝１１２．５（ｍ/分） |
| Ｂが点検している間、Ａのみが10分間上っていくので、Ｂが出発したときＡはふもとから 90×10 = 900mの地点にいる。 |
| のこり 3600 - 900 = 2700mをＢとＡが同時に進むので Ｂが出発して2700÷(90 + 112.5)分後にすれちがう。 |
| よって AとBがすれ違うのは ふもとから 900 + 2700÷20.25×90 = 2100m の地点。 |
| 別解：距離の比で求める |
| BがAと同時に出発すると、Bは3600mを32分間で進むので、10分間では 3600÷32×10 = 1125m 余計に進むことになる。 |
| よって AとBが同時出発して出会うには AとBの距離の比は (1)より４：５ なので 3600 + 1125 = 4725m をAが④、Bが⑤の割合で進めばよい。 |
| AとBが最初にすれ違うのはふもとから ４７２５÷９×４＝２１００ｍの地点。 |
| 答 ２１００ｍ |
| (3) 2台が最初にすれ違うのが、山の頂上とふもとのちょうど中間の1800mの地点になるのは、どちらが何分おくれて出発した場合ですか。 |
| 解説 |
| Aは上りで速さは分速90mなので、1800m進むのにかかる時間は 1800÷90 = 20(分) |
| Bは下りので速さは分速112.5mなので、1800m進むのにかかる時間は 1800÷112.5 = 16(分) |
| よって 山の頂上とふもとのちょうど中間の1800mの地点ですれ違うためには Bが 20 - 16 = 4(分)おくれて出発した場合。 |
| 別解 |
| AとBの速さの比は4：5 よって 距離の比も 4：5 |
| Ａは1800m進み間にBは1800÷4×5 = 2250m進むと考えると Bは2250 - 1800 = 450m余計に進むので。 |
| Bが450m進むのにかかる時間は 450÷112.5 = 4分 |
| 答 Bが４分おくれて出発した場合。 |
