麻布中学校算数過去問研究
2024年度麻布中学校入学試験は募集人数300名に対し、応募者は826名，受験者数796名 合格者352名，最高点152点，最低点105点でした。
算数入試問題は 昨年同様大問6題の出題でした。
出題内容は １．四則計算 ２．平面図形 ３．流水算 ４．規則性 ５．旅人算 ６．数の性質でした
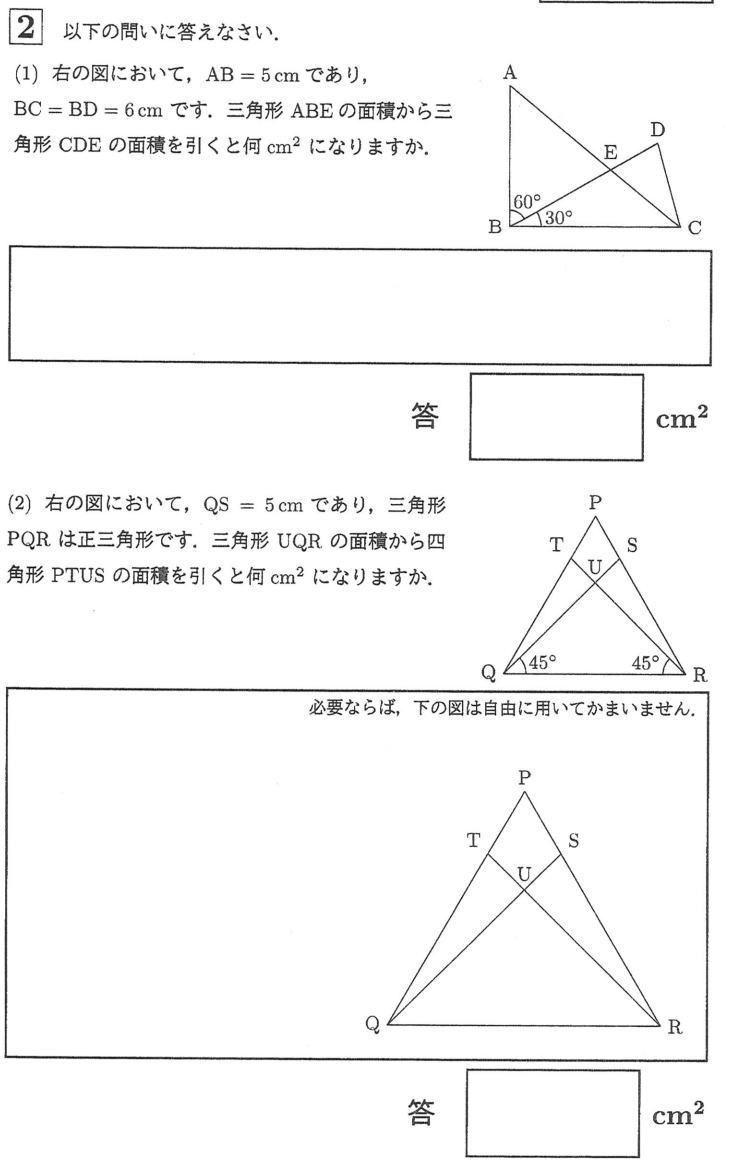
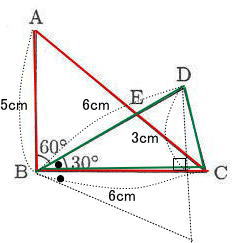
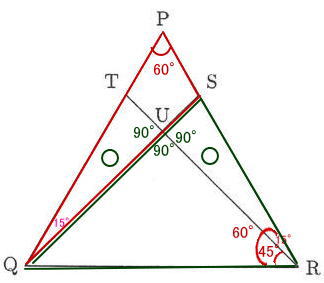
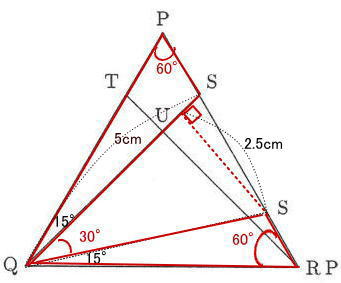
今回は ２ 平面図形を解説します。閃くとすぐ解ける問題です。
麻布中学校合格のための過去問傾向と対策
麻布中学校・高等学校過去問対策
男子御三家中学受験指導はスペースONEのプロ家庭教師にお任せください。
麻布中学校2024年度算数入試問題2.平面図形 問題
麻布中学校2024年度算数入試問題2.平面図形 (1)解説解答
解説解答
三角形ABC = 三角形ABE + 三角形EBC
三角形DBC = 三角形CDE + 三角形EBC
三角形EBCが共通なので
三角形ABC - 三角形DBC = 三角形ABE - 三角形CDE
三角形DBCは底辺6cm高さ3cmなので
6×5÷2 - 6×3÷2 = 3×(5 - 3) = 6
答え 6c㎡
麻布中学校2024年度算数入試問題2.平面図形 (2)解説解答
解説解答
三角形SQR = 三角形UQR + 三角形SUR
三角形PQS = 四角形PTUS + 三角形TQU
三角形SQR - 三角形TQU = 三角形UQR + 三角形SUR - (四角形PTUS + 三角形TQU)
三角形TQUと三角形SRUは合同な三角形なので
三角形SQR - 三角形TQU = 四角形PTUS
三角形PQSは 角SPQ = 60° 角PQS = 60° - 45° = 15° PQ = RQなので
上図のように 三角形PQSを重ねると 面積の差は底辺5cm高さ2.5cmの三角形の面積 5×2.5÷2 = 6.25
答え 6.25c㎡
プロ家庭教師集団スペースONEの麻布中学合格のための過去問対策へプロ家庭教師集団スペースONEの中学受験過去問対策へ