
穎明館中学校算数問題研究
2018年度穎明館中学校算数入試問題から平面図形を解説します。三角形の相似比を用いて解きます。対応する辺を間違いないようなれないうちは色分けするなどをして練習をしましょう。
算数入試問題 3.平面図形にチャレンジ

難関中学受験指導はスペースONEのプロ家庭教師にお任せください。

算数入試問題 3.平面図形にチャレンジ
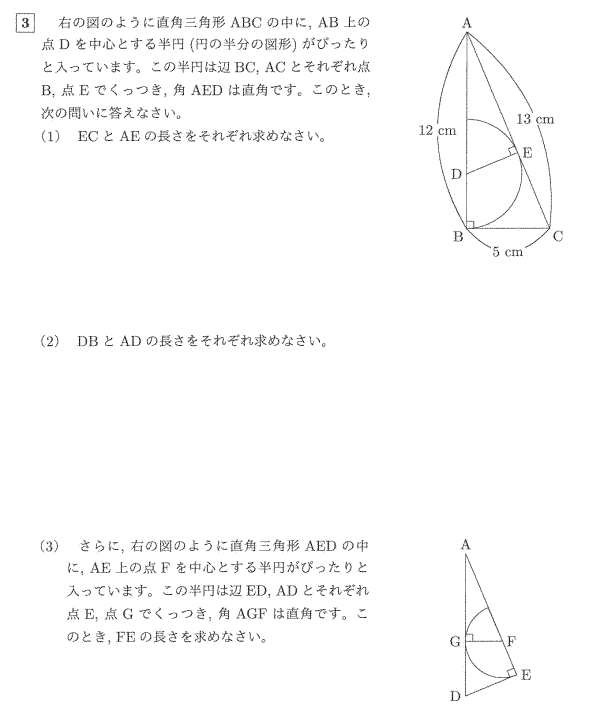
| (1) ECとAEの長さをそれぞれ求めなさい。 |
| 解説 |
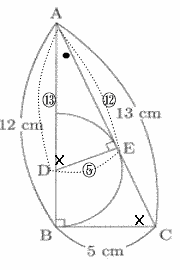 |
| 角ABC = 角AED = 90°,角CAB = 角DAE なので、三角形ABCと三角形AEDは相似形。 各辺の比は AB:BC:CA = ⑬:⑤:⑫ また、DB = ED(半径) なので、DB = ⑤ ⑬ + ⑤ = ⑱ = 12cm EC = AC - AE = 13 - 8 = 5cm |
| 答え EC = 5cm,AE = 8cm |
| (2) DBとADの長さをそれぞれ求めなさい。 |
| 解説 |
| (1)より、DB = DE = ⑤ |
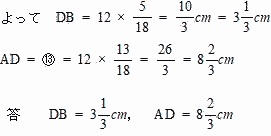 |
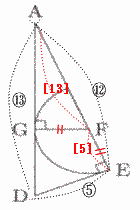
| (3) さらに、右の図のように直角三角形AEdの中に、AE上の点Fを中心とする半円がぴったりと入っています。この半円は辺ED、ADとそれぞれ点E,点Gでくっつき、角AGFは直角です。このとき、FEの長さを求めなさい。 |
 |
| 解説 |
| 三角形ADEと三角形AFGは 角DEA = 角FGA = 90° 角EAD = 角FGA (共通) なので、三角形ADEと角AFGは相似形 (1),(2) より 三角形ADEの辺の比は 三角形AFGの辺の比もAF:FG:GA = 13:5:12 また FG:FE (半径) なので、AF:FE = 13:5 AE = 8cmなので、 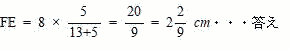 |