
東洋英和女学院中等部過去問研究
2010年度東洋英和女学院中等部A日程算数入試問題は1.四則計算3問,2.小問集合5問,3.平面図形の求積, 4.年齢算 5.虫食い算2問 6.約束(場合の数) 7.立体上の点移動 8.立体の体積 9.文章題 の構成でした。
算数の合格者最高点100点,合格者最低点 54点 合格者平均点79.6点でした。
今回は7.立体上の点移動を解説します。

難関中学受験指導はスペースONEのプロ家庭教師にお任せください。

東洋英和女学院中等部過去問研究
2010年度東洋英和女学院中等部A日程算数入試問題は1.四則計算3問,2.小問集合5問,3.平面図形の求積, 4.年齢算 5.虫食い算2問 6.約束(場合の数) 7.立体上の点移動 8.立体の体積 9.文章題 の構成でした。
算数の合格者最高点100点,合格者最低点 54点 合格者平均点79.6点でした。
今回は7.立体上の点移動を解説します。
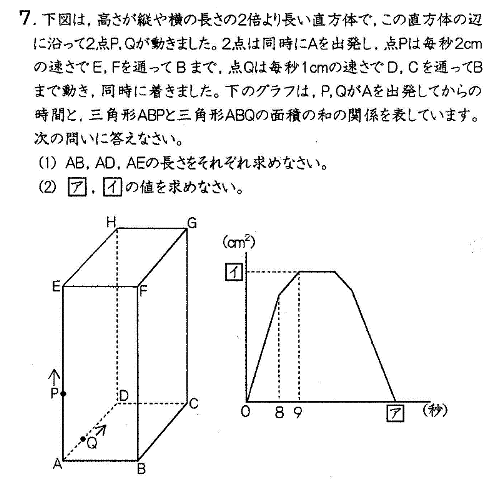
(1) AB,AD,AEの長さをそれぞれ求めなさい。
解説解答
三角形APBの面積は、PがEに着くまでは徐々に増え、EF間は一定、FからBに行くに従って減っていき、Bに着いたとき0になる。同様に三角形APBの面積は、QがDに着くまでは徐々に増え、DC間は一定、CからBに行くに従って減っていき、Bに着いたとき0になる。
AEの長さはADの長さの2倍以上あるので、出発して8秒後のグラフの傾きの変化はQがDに着いたことを示す。よってADの長さは1×8=8cm。9秒後から面積が一定になるので、AEの長さは2×9=18cm
Pの通り道はA→E→F→B, Qの通り道はA→D→C→B, EF=DC, AE=FB, AD=CBより
PはEF+DCを18秒間で、QはAE+FBを16秒間で進む。
EF=DCを進むときのPとQの速さの比は②:①なので、時間の比は①:②
PQともAを出発して同時にBに着いたので、18-16=2秒が時間の比の差 ①に相当する。
よって EF間とDC間を進むときにかかった時間はそれぞれPは2×①=2秒, Qは2×②=4秒
EF=DC=ABの長さは 4cm
答 AB=4cm, AD=8cm, AE=18cm
(2) (ア)(イ)の値を求めなさい。
解説解答
(ア) PQが同時にBに着く時間なので、
(1)より AE=BF=9秒, EF=2秒。
よって 9×2+2=20秒(イ)
PがEF間, QがDC間を進んでいるときの三角形ABPと三角形ABQの面積の和なので、
三角形ABP=4×18÷2=36c㎡, 三角形ABQ=4×8÷2=16c㎡
よって (イ)=36+16=52c㎡
答 (ア)20 (イ)52