富士見中学校算数過去問研究
富士見中学校では、2020年2月2日の午後に算数1教科入試を実施いたします。
校長と数学科からのメッセージです。
校長メッセージ
2020年度入試より「論理的に考える力」を重視した「算数1教科入試」を導入します。試験時間を長くした「算数1教科入試」では、受験生のみなさんがこれまで培ってきた考える力を存分に発揮できます。
富士見では、「論理的に考える力」は、あらゆる課題を解決する中で必要な力だと考えています。それは、4教科入試においても「丸暗記」した知識を問わないことからお分かりいただけるでしょう。じっくり問題に向き合うことで、「論理的に考える力」は育まれます。矛盾や飛躍がないか、複雑なことがらをわかりやすく示しながら、結論を導き出せているかといったことが大切です。
来年の4月は、算数1教科入試だけでなく4教科入試、帰国生入試の入学生が一緒に学校生活をスタートします。お互いに刺激しあいながら、自分を磨く場所が、ここ富士見にはあります。
数学科より受験生のみなさんへ
算数1教科入試では、文章から問題を解くのに必要なことがらを読み取り、論理的に組み立てて結論を出す問題や、データや表を読み取って考える問題、実際にグラフや図を描く問題などを出題します。
大問は3問で分野に偏りはありませんが、問題文を読み、様々な計算を試したり、積極的に図や表を書く力を必要とする問題が中心です。一見すると午前の4教科入試の問題傾向とは異なるように見えるかもしれません。しかし、基本的な解き方や計算力を組み合わせ、論理的に考えることで答えにたどり着けます。普段から答えだけではなく、答えにたどり着くまでの考え方を大切にしましょう。
2016年度富士見中学校の算数入試問題は例年通りの出題構成で、内容は1.小問集合8問,2.小問2問 3.平面図形の分割 4.速さと数の性質でした。解答形式は3.(3)のみが途中式や考え方を書き、他は解答のみを書く形式でした。
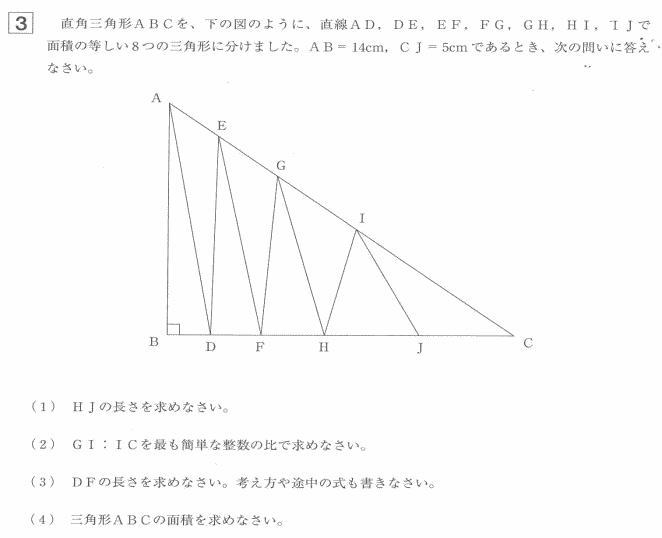
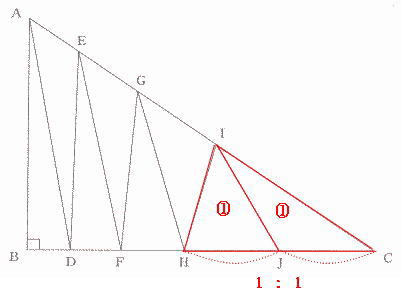
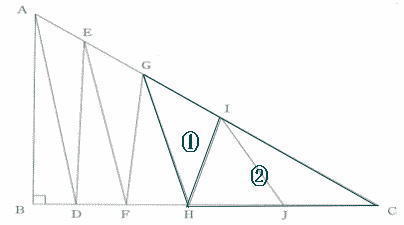
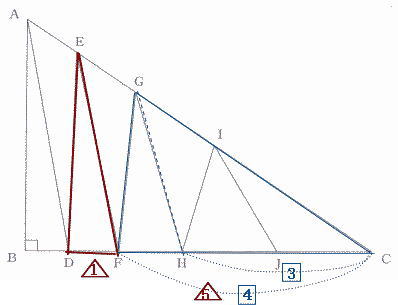
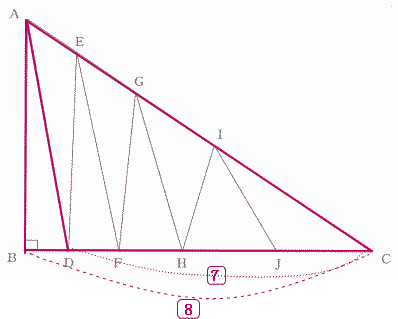
今回は 3.平面図形の分割を解説します。
算数入試問題3.平面図形の分割にチャレンジ