中学受験はプロにお任せ/プロ家庭教師集団スペースONEの明治学園中学校合格のための過去問傾向と対策2015年度算数入試問題小問集合

明治学園中学校・高等学校過去問対策

中学受験指導はスペースONEのプロ家庭教師にお任せください。

明治学園中学校合格のための過去問対策

明治学園中学校過去問研究

2015年度　明治学園中学校算数入試問題は　例年通り小問集合・大問5題の出題構成で1.した。出題内容は1.小問集合10問，2.約束記号3.割合の文章題　4.場合の数　5.速さでした。

今回は　スペースＯＮＥ福岡校のプロ家庭教師が1.小問集合を解説します。

算数入試問題

明治学園中学校2015年度算数入試問題1.小問集合　問題

明治学園中学校2015年度算数入試問題1.小問集合　四則演算解説解答

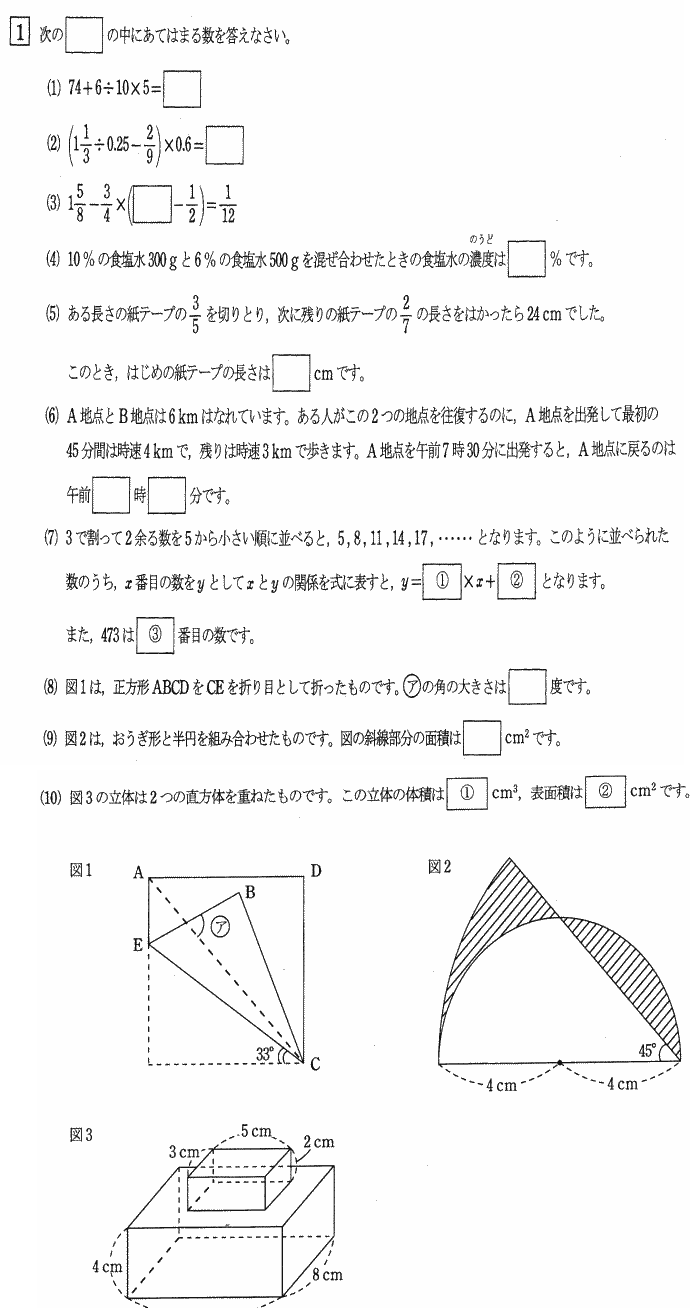
(1) 74 + 6÷10×5 =
解答


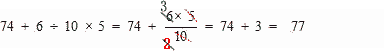答　　77

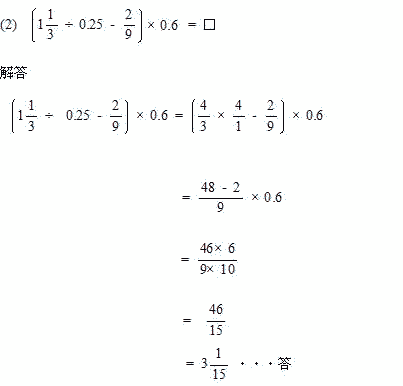
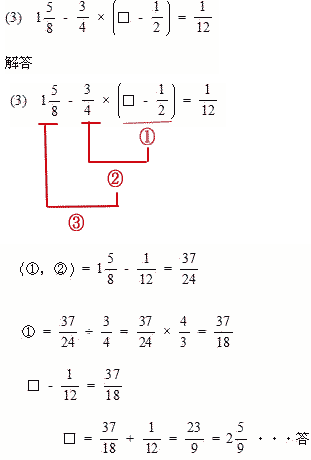
明治学園中学校2015年度算数入試問題1.小問集合(4)食塩水の濃度解説解答

(4)　10%の食塩水300gと6%の食塩水500gを混ぜ合わせたときの食塩水の濃度は□%です。

解説

10%の食塩水300gに含まれる食塩の量は　300×0.1 = 30g

6%の食塩水500gに含まれる食塩の量は　500×0.06 = 30g

よって混ぜ合わせたときの食塩の量は30 + 30 = 60g　　食塩水の量は300 + 500 = 800g

したがって　濃度は　60÷800 = 0.075 = 7.5%

答　　　7.5％

明治学園中学校2015年度算数入試問題1.小問集合(5)相当算解説解答

明治学園中学校2015年度算数入試問題1.小問集合(6)旅人算解説解答

(6)　A地点とB地点は6kmはなれています。ある人がこの2つの地点を往復するのに、A地点を出発して最初の45分間は時速4kmで、残りは時速3kmで歩きます。A地点を午前7時30分に出発するとA地点に戻るのは午前□時□分です。

解説

A地点とB地点間を往復する12kmを進むのにかかる時間を考えるとよい。A地点を出発して最初の45分間は時速4kmで進む距離は　

残り　12 - 3 = 9mを時速3kmで進むのにかかる時間は

9÷3 = 3時間

よって　午前7時30分に出発すると3時間45分後にA地点に戻るので、午前11時45分

答　　午前11時45分

明治学園中学校2015年度算数入試問題1.小問集合(7)関係式解説解答

(7)　3で割って2余る数を5から小さい順に並べると　5, 8, 11, 14, 17・・・となります。このように並べた数のうち、χ番目の数をyとして、χとyの関係を式に表すと、y = □×χ + □となります。また、473は□番目の数です。
解説
5 = 3×1 + 2，　　　8 = 3×2 + 1，　　　　11 = 3×3 + 2　　となるので、 y = 3×χ + 2
473 = 3×□ + 2 より　□ = (473 - 2)÷3 = 157

答　　 y = 3×x + 2　, 473は157番目の数

明治学園中学校2015年度算数入試問題1.小問集合(8)折り返し図形解説解答

(8) 図1は、正方形ABCDをCEを折り目として折ったものです。(ア)の角の大きさは□度です。
解説
Bの折り返す前の頂点をFとする。角ECF = 角ECB = 33°，ACは正方形の対角線なので、角ACF = 45° よって　角ACB = 33×2 - 45 = 21°角CBE = 90° したがって　(ア) = 90 - 21 = 69°

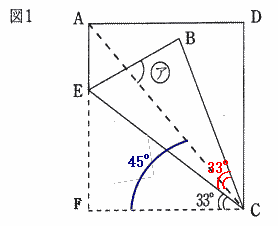答　　　69°

明治学園中学校2015年度算数入試問題1.小問集合(9)等積変形解説解答

(9)　図2はおうぎ形と半円を組み合わせたものです。図の斜線部分の面積は□c㎡です。
解説
図のように等積変形する。求める面積 = (半径8cm,中心角45°のおうぎ形の面積) - (底辺8cm高さ4cmの三角形の面積)

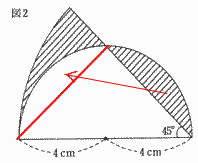答　　　9.12c㎡

明治学園中学校2015年度算数入試問題1.小問集合(10)立体図形解説解答

(10)　図3の立体は2つの直方体を重ねたものです。この立体の体積は□cm³，表面積は□cm²です。

解説

体積は底面積（たて8cm, 横10cm），高さ4cmの直方体の体積 + 底面積（たて3cm，よこ5cm）高さ2cmの直方体の体積

よって　8×10×4 + 3×5×2 = 350cm³

表面積：底面積（たて8cm,よこ10cm）たかさ4cmの直方体の表面積より斜線部の面積のみ大きくなる。

したがって　10×8×2 + (10 + 8)×2×4 + (% + 3)×2×2 = 336cm²

答　　体積　　350cm³　　　表面積　336cm²