明治学園中学校過去問研究
2015年度 明治学園中学校算数入試問題は 例年通り小問集合・大問5題の出題構成で1.した。出題内容は1.小問集合10問，2.約束記号3.割合の文章題 4.場合の数 5.速さでした。
今回は スペースＯＮＥ福岡校のプロ家庭教師が5.速さを解説します。
算数入試問題
明治学園中学校合格のための過去問対策
明治学園中学校・高等学校過去問対策
中学受験指導はスペースONEのプロ家庭教師にお任せください。
明治学園中学校2015年度算数入試問題5.旅人算 問題
明治学園中学校2015年度算数入試問題5.旅人算(1)解説解答
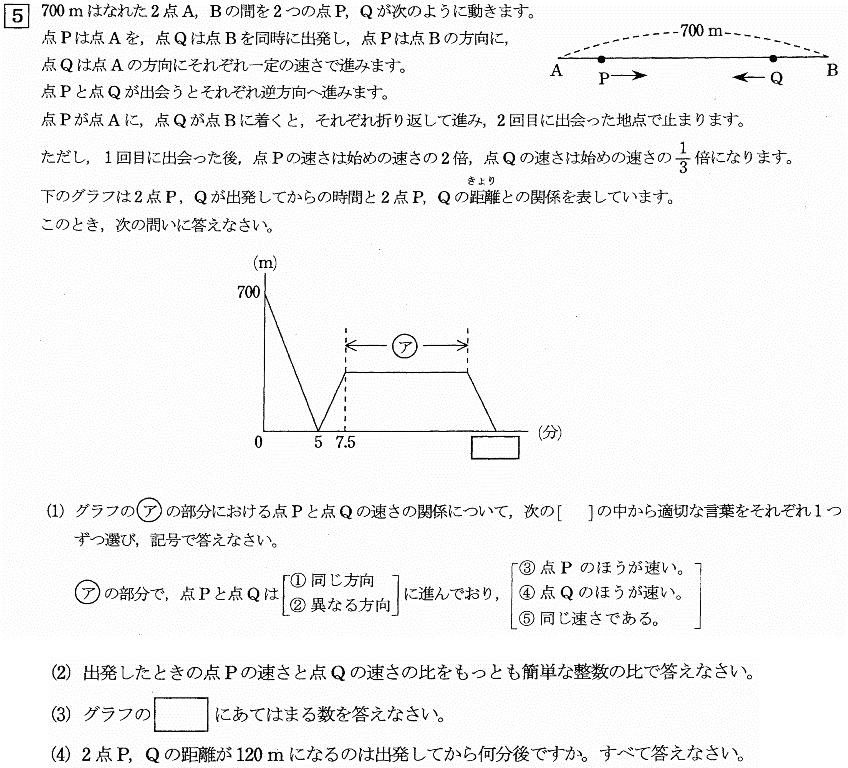
| (1) グラフの(ア)の部分における点ＰとＱの速さの関係について、次の[ ]の中から適切な言葉をそれぞれ１つずつ選び、記号で答えなさい。 (ア)の部分で、点Ｐと点Ｑは（① 同じ方向，② 異なる方向）に進んでおり、（③ 点Ｐのほうが速い。 ④ 点Ｑのほうが速い。 ⑤ 同じ速さである） |
|
| 解答 | |
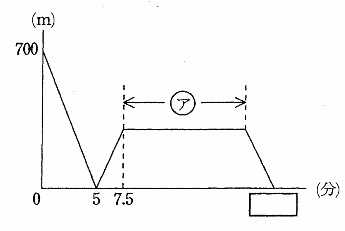
| グラフより | |
 |
|
| 点Ｐと点Ｑが同時に出発して5分後に出会い、その後それぞれが引き返し、ＰまたはＱが元の出発地点に7.5分後に着き、(ア)の部分で着いた方が相手を追いかけて同じ方向に進んでいる。(ア)の部分ではＰとＱの間の距離は変わらないので、ＰとＱは同じ速さである。 | |
| 答 ① ，⑤ | |
明治学園中学校2015年度算数入試問題5.旅人算(2)解説解答
| (2) 出発したときの点Pの速さと点Qの速さの比をもっとも簡単な整数の比で答えなさい。 |
| 解答 |
 |
| 答 点Pの速さ：点Qの速さ = 1：6 |
明治学園中学校2015年度算数入試問題5.旅人算(3)解説解答
 (3) グラフの□にあてはまる数を答えなさい。 |
| 解説 |
|
| □は点Pと点Qが出発して2回目に出会う時間。 |
| 点Pと点Qが1回目に出会うのは出発して5分後なので、点Pと点Qの速さの和は 700÷5 = 140(m/分) 点Pの速さ：点Qの速さ = 1：6なので、距離の比も1：6 1回目に出会うまでに点Pは 700÷7 = 100m進んで、Aまで7.5 - 5 = 2.5分で戻っているので 点Pが速さを変えた後の分速は100÷2.5 = 40m 点Qも同じ速さで分速40m 図の通り |
 |
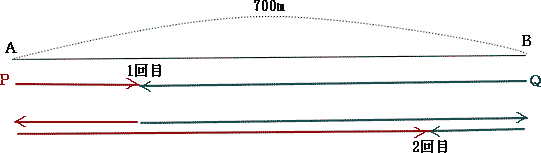| 点Pと点Qは1回目に出会ってから2回目に出会うまでに700×2 = 1400m進んでいるので、 |
| 2回目に出会うまでの時間は 1400÷（40×2) = 17.5分 したがって 2回目に出会うのは、出発して 5 + 17.5 = 22.5分 |
| 答 22.5 |
| 別解 |
 |
| 出会った後の速さは 20×2 = 40(m/分) 図の通り |
|
| 点Pと点Qは1回目に出会ってから2回目に出会うまでに700×2 = 1400m進んでいるので、 |
| 2回目に出会うまでの時間は 1400÷（40×2) = 17.5分 したがって 2回目に出会うのは、出発して 5 + 17.5 = 22.5分 |
| 答 22.5 |
明治学園中学校2015年度算数入試問題5.旅人算(4)解説解答
| (4) 2点P，Qの距離が120mになるのは出発してから何分後ですか。すべて答えなさい。 | |
| 解答 | |
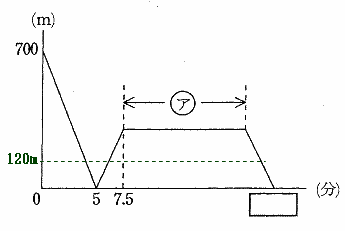
| グラフより2点P，Qの距離が120mになるのは出発してから3回。 | |
 |
|
| 1回目 AB間を120mまで近づいたとき。点Pと点Qのはじめの速さの和は分速140mなので、 |
|
 |
|
| 2回目 点Pと点Qが1回目に出会って、それぞれが元の位置に戻る途中120mはなれたときなので、 1回目に出会って 120÷（40×2） = 1.5分後 したがって 出発後 5 = 1.5 = 6.5分後 |
|
| 3回目 点QがBに戻って、点Pと2回目に出会う途中。2回目に出会う時間は出発後22.5分。出会うまでに120mの距離を縮めるのに2回目と同様1.5分かかるので、 3回目に点Pと点Qの間が120m離れていたのは 22.5 - 1.5 = 21分後、 |
|
 |
|