学習院女子中等科算数過去問研究
2013年度 算数Ａ入試問題は [1] 計算2問（四則計算，連比） [2] 場合の数 [3] 速さ [4] 平面図形（相似形応用） [5] 数列 ［6］ 平面図形の変形が出題されました。
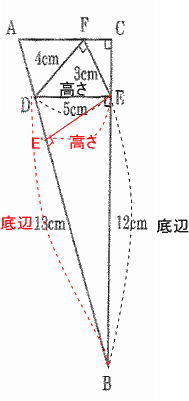
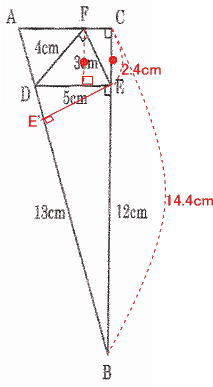
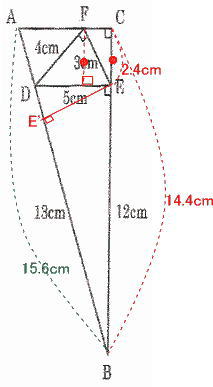
今回は [4] 平面図形（相似形応用）を解説します。（１）の設問が（２）の解法のヒントになっています。題意をくみ取って解きましょう。
算数入試問題 平面図形にチャレンジ
学習院女子中等科合格のための過去問傾向と対策
学習院女子中等科・高等学校過去問対策
中学受験指導はスペースONEのプロ家庭教師にお任せください。
学習院女子中等科2013年度算数入試問題4.平面図形 問題
学習院女子中等科2013年度算数入試問題4.平面図形(1)解説解答
(1) 直角三角形ＤＢＥの底辺を辺ＤＢとするとき、この三角形の高さを求めなさい。
解説
点Ｅから辺ＤＢに垂線をおろし、その交点をＥ’とする。直角三角形ＤＢＥの底辺を辺ＥＢとしたときの高さはＤＥなので
辺ＥＢ×辺ＤＥ＝辺ＤＢ×辺ＥＥ’
１２×５＝１３×辺ＥＥ’
辺ＥＥ’＝60/13
答 60/13 cm
学習院女子中等科2013年度算数入試問題4.平面図形(2)解説解答
解説
三角形ＡＢＥの底辺をAＢとしたときの高さはＥＥ’。よって ＡＢの長さを求めると良い。
三角形ＤＢＥと三角形ＡＢＣは相似形なので、辺ＢＥ：辺ＢＣの相似比＝辺ＢＤ：辺ＢＡの相似比
直角三角形ＦＤＥにおいて、点Ｆから辺ＤＥに垂線をおろしその交点をＦ’とすると、辺ＦＦ’＝辺ＣＥ
よって 辺ＣＥ＝辺ＦＦ’＝３×４÷５＝２．４（ｃｍ）
１２：１２＋２．４＝１３：辺ＢＡ
辺ＢＡ＝14.4×13÷12
よって 三角形ＡＢＥの面積は （14.4×13÷12）×（12×5÷13）÷２＝14.4×5÷2＝３６
答 ３６ｃ㎡
学習院女子中等科2013年度算数入試問題4.平面図形(3)解説解答
(3) 辺ＡＤの長さを求めなさい。
解説
辺ＡＢー辺ＤＢ＝辺ＡＤよって 14.4×13÷12ー13＝２．６
答 ２．６ｃｍ