中学受験指導専門プロ家庭教師の学習院中等科過去問研究
学習院中等科受験指導はスペースONEのプロ家庭教師にお任せください。
 |
ご依頼専用ダイヤル |
0120-604-405 |
| お問い合わせ |
03-6868-6040 |
 |
お問い合わせメール
|
|
 |
ws-spaceone |
|
 プロ家庭教師集団スペースONE
プロ家庭教師集団スペースONE
中学受験案内HOME
 インターネット指導コース
インターネット指導コース
2011年度学習院中等科算数入試問題(過去問) 解答解説
学習院中等科過去問研究
2011年度学習院中等科算数入試問題は1.計算4問、2.小問集合 3.平面図形(面積比と辺の比) 4.旅人算のグラフ 5.立体図形の分割 6.場合の数 が出題されました。例年通り、大問はダイヤグラム、整数の性質、速さの比、場合の数、平面図形が出されました。問題傾向に大幅な変更はなく過去問研究が大切な受験校です。
今回は 2.平面図形(面積比と辺の比)を解説します。
算数入試問題(整数の性質にチャレンジ)
問題 2
スペースONEプロ家庭教師の解答で、学習院中等科の発表ではありません。
(1)解説解答
| 三角形RPCの面積を求めなさい。 |
|
| 解説 |
|
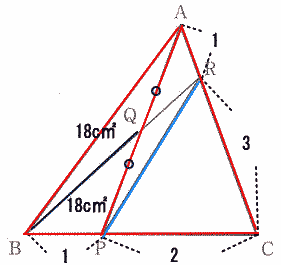
 三角形QBPの面積は18c㎡ 三角形QBPの面積は18c㎡
QはAPの真ん中の点なので
△QBP=△QBA=18c㎡
BP:PC=1:2より
△BAP:△PAC=1:2
△BAP=△QBP+△QBA=18×2=36c㎡なので
△PAC=36×2=72c㎡
AR:RC=1:3より
△APR:△RPC=1:3
△RPC=3/4△PAC
=72×3/4=54 |
 |
|
|
| 答 54c㎡ |
|
|
|
(2)解説解答
| BQ:QRを求めなさい。ただし、最も簡単な整数の比で答えなさい。 |
|
|
|
| 解説 |
|
|
|
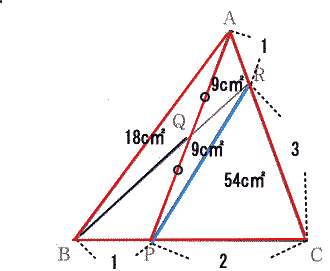
(1)より △APR=1/4△PAC=72×1/4=18c㎡
AQ:QP=1:1 なので △AQR=18÷2=9c㎡
△ABQ:△AQR=18:9=2:1
よって BQ:QA=2:1 |
 |
|
|
| 答 2:1 |
|
|
|
|
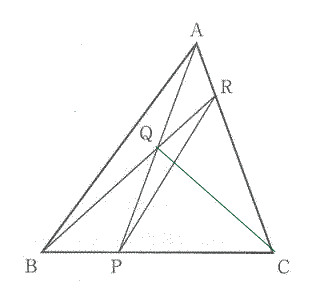
(2)別解
| BQ:QRを求めなさい。ただし、最も簡単な整数の比で答えなさい。 |
|
|
|
| 解説 |
|
|
|
(1)より △APR=1/4△PAC=72×1/4=18c㎡
AQ:QP=1:1 なので △AQR=18÷2=9c㎡
△ABQ:△AQR=18:9=2:1
よって BQ:QA=2:1 |
 |
|
|
| 答 2:1 |
|
|
|
|
|
HOME
このホームページのすべての文章の文責および著作権はプロ家庭教師集団スペース ONEに属します。