市川中学校過去問対策
2024年度市川中学校第1回入学試験は、1月20日に実施され、募集人数男子180名 女子100名に対し 応募者男子1731名 女子890名 受験者男子1675名 女子862名 合格者男子745名 女子288名 合格最高点男子336点 女子319点
合格者最低点227 227でした。
教科別受験者平均点は 国語男子55.4点 女子58.5点 算数男子46.2点 女子40.4点 社会男子62.6点 女子59.5点 理科56.6点 女子53.6点でした。
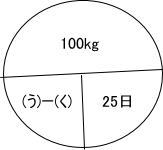
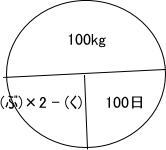
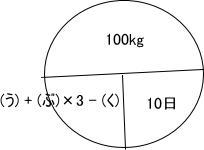
算数入試問題は、例年通りの出題構成でした。出題内容は[1]小問集合5問，[2] 約束記号，[3] 平面図形(円に内接する円の問題)，[4] 時計算，[5] ニュートン算でした。
今回は 5.ニュートン算を解説します。速さの三公式の追いかけ算の考え方を用いて解きましょう。
市川中学受験指導はスペースONEのプロ家庭教師にお任せください。
