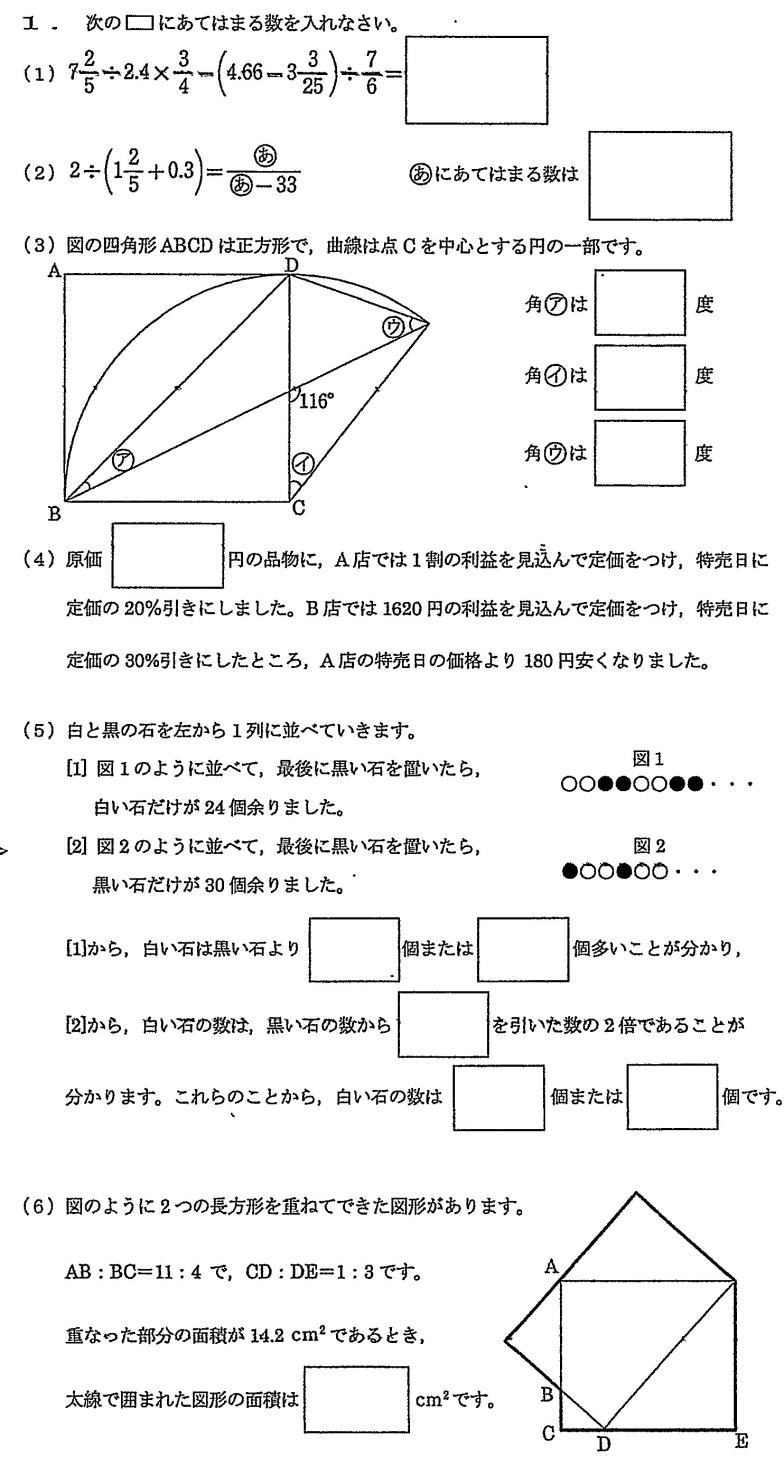
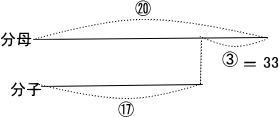
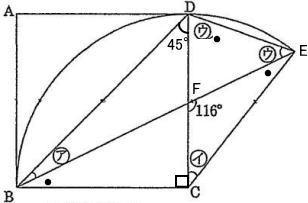
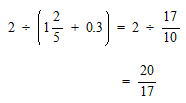女子学院中学校・高等学校過去問対策

女子御三家中学受験指導はスペースONEのプロ家庭教師にお任せください。

女子学院中学校合格のための過去問対策

girl

女子学院中学入試問題出題傾向と対策

2021年度女子学院中学校入学試験は、募集人数第一学年240名，受験資格が「親元から通学でき、通学に要する時間が通常の交通機関を持ちて90分いないの者」。

選抜方法は　筆記試験「国語・算数・理科・社会」各40分 100点満点。本人のみのグループ面接5人程度で約10分間。小学校長の報告書」でした。

算数入試問題は、例年通り大問6題構成で、1.四則計算を含む小問集合6問 　2.数の性質　3.ニュートン算とつるかめ算　4.図形　5.場合分け　6.速さが出題されました。　
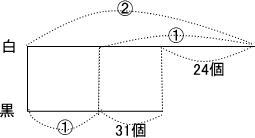
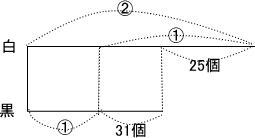
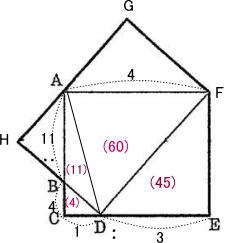
今回は　1.小問集合(2)～(6)を解説します。

女子学院中学校2021年度算数入試問題　1.小問集合　問題

女子学院中学傾向と対策


女子学院中学校2021年度算数入試問題　1.小問集合 (2)　数の性質　解説解答

女子学院中学校算数入試傾向と対策

解説解答

女子学院中学受験プロ家庭教師東京

線分図で表すと

プロ家庭教師東京

③ = 33 　なので　① = 11

(あ) = ⑳ = 11×20 = 220

答　220

女子学院中学校2021年度算数入試問題　1.小問集合 (3)　平面図形　解説解答

(3)　図の四角形ABCDは正方形で、曲線は点Cを中心とする円の一部です。

解説解答

図のように点E，Fとする。

中学受験プロ家庭教師東京

角BFD = 116°，角BDC = 45°(三角形BDCは直角二等辺三角形)
よって　角ア = 180 - (116 + 45) = 19°

角FBC = 角DBC - 角ア = 45 - 19 = 26°
三角形BECは二等辺三角形なので　角BFC = 26°
角イ = 角BCE - 角BCF = 180° - 26×2 - 90 = 38°

三角形DCEは二等辺三角形
角DEC = (180 - 38)÷2 = 71°
角ウ = 71 - 角FEC = 71 - 26 = 45°

答　　角ア　19°，角イ　38°，角ウ　45°

女子学院中学校2021年度算数入試問題　1.小問集合 (4)　損益売買　解説解答


(4)　原価□円の品物に、A店では1割りの利益を見込んで定価をつけ、特売日に定価の2割引にしました。B店では1620円の利益を見込んで定価をつけ、特売日に定価の30%引きにしたところ、A店の特売日の価格より180円安くなりました。

解説解答

原価を(1)とする。A店の特売日の価格は　(1)×(1 + 0.1)×(1 - 0.2) = (0.88)

B店の特売日の価格は　((1) + 1620}×(1 - 0.3) = (0.7)+1134

A店の特売日の価格よりB店の特売日の価格は180円安いので、

(0.88) = (0.7) + 1134 + 180
(0.18) = 1314
(1) = 1314÷0.18 = 7300

答　　7300円

女子学院中学校2021年度算数入試問題　1.小問集合 (5)　数の性質　解説解答

(5)　白と黒の石を左から1列に並べていきます。

[1]図1のように並べて、最後に黒い石を置いたら、白い石だけが24個残りました。

　　　図1
　　○○●●○○●●・・・

[2]図2のように並べて、最後に黒い石を置いたら、黒い石だけが30個残りました。

　　　図2
　　●○○●○○・・・

[1]から、白い石は黒い石より□個または□個多いことがわかり、[2]から、白い石の数は、黒い石の数から□を引いた数の2倍であることがわかります。これらのことから、白い石の数は□個または□個です。

解説解答
[1]　最後においた黒い石が1個のとき

　　　図1
　　・・・｜　○○●●　｜　○○●　　　　　白い石が黒い石より24 + 1 =25個多い
　　　　　　　差なし　　　白が1個多い

[1]　最後においた黒い石が1個のとき

　　　図1
　　・・・｜　○○●●　｜　○○●●　｜　　　　　白い石が黒い石より24 個多い
　　　　　　　差なし　　　差なし

[2]図2のように並べて、最後に黒い石を置いたら、黒い石だけが30個残りました。

　　　図2
　　●○○｜●○○｜・・・ 　白石が黒石の2倍＋黒石30個
黒石と白石の数の比
　　1：2

(1)　白い石が黒い石より24個多いとき
① = 31 + 24 = 55
算数専門プロ家庭教師
白 = ② = 55×2 = 110個

(2)　白い石が黒い石より25個多いとき
① = 31 + 25 = 56
プロ家庭教師東京中学受験
白 = ② = 56×2 = 112個

答　 [1]から、白い石は黒い石より[24]個または[25]個多いことがわかり、[2]から、白い石の数は、黒い石の数から[31]を引いた数の2倍であることがわかります。これらのことから、白い石の数は[110]個または[112]個です。

女子学院中学校2021年度算数入試問題　1.小問集合 (6)　平面図形の求積　解説解答

(6)　図のように2つの長方形を重ねてできた図形があります。AB：BC = 11：4で、CD：DE = 1：3です。重なった部分の面積が14.2c㎡であるとき、太線で囲まれた図形の面積は□c㎡です。

解説解答
図のように点F，G，Hをおく。
プロ家庭教師集団中学受験専門

AB：BC = 11：4なので　三角形ABDと三角形BCDの面積比は11：4

CD：DE = 1：3なので　三角形ACDと三角形FDEの面積比は1：3

三角形ACDの面積を(15)とすると、三角形FDEの面積は(15)×3 = (45)

AF：FD = 1+3：3 = 4：3なので

女子学院傾向と対策

重なった部分四角形ABDFの面積(11) + (60) = (71)が14.2c㎡なので　(1) = 14.2÷71 = 0.2c㎡

四角形ACEF = 四角形HDFGの面積は

女子学院中学受験プロ家庭教師東京

太線で囲まれた図形の面積は

四角形HDFGの面積 + 三角形BCDの面積 + 三角形FDEの面積

24 + (4 + 45)×0.2 = 24.98

答　24.98c㎡
Copyright(c) 2013 Sample Inc. All Rights Reserved. Design by http://f-tpl.com