海城学園 海城中学校帰国入試算数過去問研究
2022年度海城中学第１回入学試験は 募集人数145名に対し、応募者数656名 受験者数489名 合格者数163名でした。
教科別成績は 国語配点120点 受験者最高点106点 受験者平均点71.6点 合格者平均点82.1点。算数配点120点 受験者最高点120点 受験者平均点71.5点 合格者平均点85.1点 社会配点80点 受験者最高点66点 受験者平均点38.3点 合格者平均点44.2点 理科配点80点 受験者最高点69点 受験者平均点46.7点 合格者平均点52.6点。合格最低点245点(400点満点)でした。
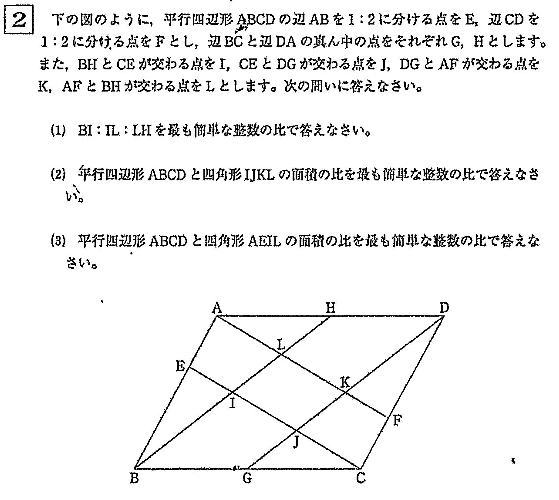
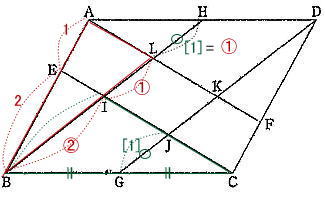
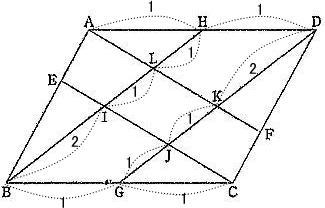
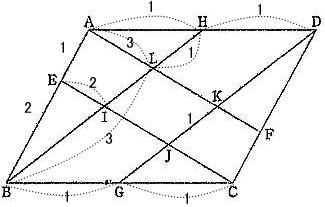
2022年度第１回算数入試問題は例年通り大問6題構成で、出題内容は1.小問集合5問 四則計算・規則性・食塩水の濃度・ニュートン算・平面図形 2.平面図形 3.速さのグラフ 4.場合の数 5.立体図形の切断6.数の性質でした。
算数入試では、分度器は使えませんが、定規・コンパスは持ち込み必須です。今回は2.平面図形を解説します。
中学受験塾のテキストでもよく出される問題です。このような定番の問題は受験者の正答率も高いと考えられます。取りこぼさないようにしましょう。
プロ家庭教師集団スペースONEの海城中学合格のための過去問対策へ