開成中学校合格のための過去問対策

2018年度　開成学園　開成中学校算数入試問題

開成学園　開成中学校過去問対策

2018年度の開成中学校算数入試問題は、[1]が例年の四則計算と一行問題から、四則計算を含む小問集合7問になり、大問3題構成に変わりました。比較的小問集合が得点源になったようで、昨年の合格者平均点 54.8点　合格者平均得点率 64.5%　から今年度は合格者平均点 73.9点　合格者平均得点率 86.9%に大幅アップしました。

今回は　1.小問集合を解説します。

開成中学校2018年度　算数入試問題　1.小問集合にチャレンジ

開成中学四則計算解説

開成中学校　2018年度算数入試問題　1.小問集合解説解答

(1) 還元算　解説解答

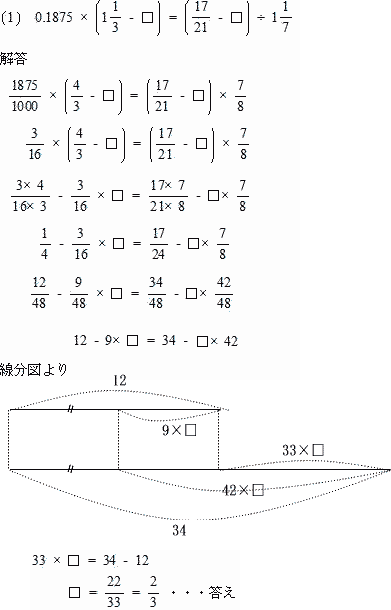（2）場合の数　解説解答

(2) 　赤球，青球，黄球が2個ずつ6個あります。同じ色の球がとなり合わないように6個すべてを左から右へ一列に並べます。このような並べ方は何通りあるか求めなさい。ただし、同じ色の球は区別しないことにします。

解説解答

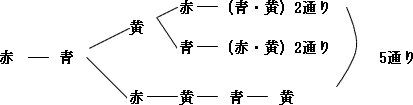左から2番目が黄球の場合も5通りあるので、左から1番目が赤球の場合の並べ方は10通り。左から1番目が青球，黄球の場合もそれぞれ10通りあるから

3×10 = 30通り

答　　　30通り

(3)　流水算　解説解答

(3)　川の上流のA町と下流のB町の間を船で往復します。A町からB町までは42分かかり、B町からA町までは1時間52分かかります。船の静水時での速さは川の流れる速さの何倍か答えなさい。船の静水での速さと、川の流れる速さはそれぞれ一定とします。

解説解答

下りにかかる時間と上りにかかる時間の比は　42分：1時間52分 = 42分：112分 = 3：8

よって　下りと上りの速さの比は　8：3

船の静水時の速さは　(8 + 3)÷2 = 5.5

川の流れの速さは　(8 - 3)÷2 = 2.5

したがって船の静水時での速さは川の流れる速さの　5.5÷2.5 = 2.2倍　

答　　2.2倍

(4)　食塩水の濃度　解説解答

	(4)　容器Ａには濃度1.62%の食塩水が600g，容器Ｂには濃度のわからない食塩水が400g入っています。Ａの食塩水のうちＮgをＢに移してよくかきまぜたのち、同じＮgをＡにもどしました。さらにまた同じことをくり返したところ、Ａ，Ｂの食塩水の濃度は順に1.88%と2.04%になりました。最初のＢの食塩水の濃度を求めなさい。
	解説解答
	Ngの食塩水をやりとりした後の容器Aと容器Bに含まれる食塩の量の合計は　600×0.188 + 400×0.204 = 194.4g やりとり前の容器Aに含まれる食塩の量は　600×0.162 = 97.2g やりとりを繰り返しても容器Aと容器Bに含まれる食塩の量の合計は変わらないので、やり取り前の容器Bに含まれる食塩の量は　194.4 - 97.2 = 97.2g 最初の容器Bの食塩水の濃度は　97.2÷400 = 0.243
	答　　24.3%

(5)　立体図形の体積　解説解答
	(5)　右の図はある立体の展開図です。Ｂ，Ｃ，Ｄは一辺が6cmの正方形，Ａ，Ｅ，Ｆは直角二等辺三角形，Ｇは正三角形です。この立体の体積を求めなさい。
	解説解答
	ある立体は一辺6cmの立方体から一辺6cmの三角すいの体積を除いた部分。したがって求める体積は

問6　正六角形の面積分割　解説解答
	(6)　面積が9c㎡である正六角形ABCDEFの各辺の中点（真ん中の点）を結んで新しい正六角形を作ります。新しい正六角形の面積を求めなさい。右の図の点Oは対称の中心です。
	解説解答
	図の通り面積を分割すると、新しい正六角形の面積は、正六角形ABCDEFの面積の3/4


問7　平面図形の面積比　解説解答
	(7)　右の図において、四角形ABCDは正方形で、BE = EF = FC，CG = GDです。 (ⅰ) 三角形AIJと四角形ABCDの面積比を最も簡単な整数の比で答えなさい。
	解説解答
	ADの延長線とBGの延長線との交点をPとする。
	三角形BIEと三角形PAI，三角形BJFと三角形PJA，三角形BGCと三角形DGPはそれぞれ相似形。


ⅱ)　四角形HIJKと四角形ABCDの面積比を最も簡単な整数の比で答えなさい。
	解説解答
	四角形HIJK の面積 = 三角形AIJの面積 - 三角形AHKの面積
	三角形BHEと三角形DHAは相似形なので、　BE：AD = BH：HD = 1：3 三角形BKFと三角形DKAは相似形なので、　BF：AD = BK：KD = 2：3