慶應義塾中等部過去問対策
2021年度慶応義塾中等部入学試験は2月3日一次試験(筆記試験) 2月4日二次試験 (一次試験合格者のみ) 体育・面接(保護者同席の面接)が実施され2月6日合格者の発表が行われました。
募集人数は男子:約140名 女子:約50名 (内部進学者の進学状況により多少の変動があります)例年男子5.6倍,女子8倍の競争率です。
教科ごとの足切りはありません。一次試験・二次試験を総合して合否を決定します。
慶応義塾中等部算数入学試験は、試験時間は45分,配点100点です。
2021年度は【1】小問集合4問(四則計算・還元算・暦・縮尺【2】小問集合5問(濃度・割合・年齢算・仕事算・時計算)【3】小問集合図形4問(比・角度・円・回転図形)【4】旅人算向かい合って歩く差のグラフ【5】条件整理【6】規則性が出題されました。
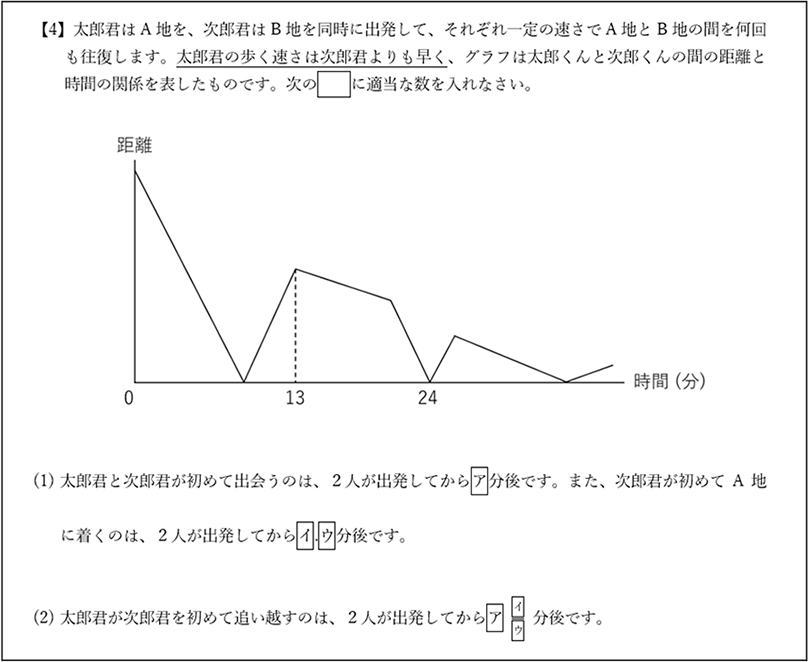
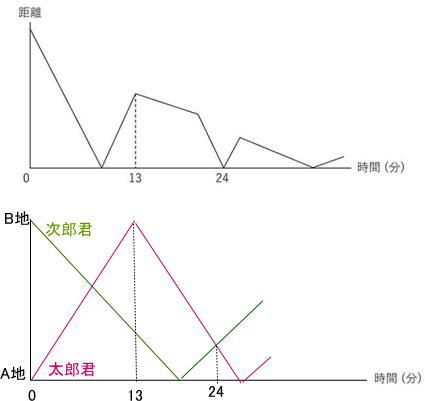
今回は2021年度算数入試問題から4.速さの出会い算のグラフ問題を解説します。