慶應義塾中等部過去問対策
2023年度慶応義塾中等部入学試験は2月3日一次試験(筆記試験算数・国語・理科・社会) 2月4日一次合格発表 2月5日二次試験 （一次試験合格者のみ） 体育・面接（保護者同席の面接）が実施され2月6日合格者の発表が行われました。
募集人数は男子：約140名(昨年比20名減) 女子：約５０名(昨年比10名減) （内部進学者の進学状況により多少の変動があります）。教科ごとの足きりはありません。一次試験・二次試験を総合して合否を決定します。
2023年度志願者数 男子 851名 女子445名 合格者 男子135名 女子58名でした。
2024年度慶応義塾中等部受験資格は、 下記のア、イのいずれかに当たる者。
ア ２０２４年３月に小学校、またはこれと同等の学校を卒業見込みの者。
イ 次の（１）（２）の条件を共に満たしている者。
（１）２０１１（平成２３）年４月２日から２０１２（平成２４）年４月１日までに生まれた者。
（２）海外に在住し、２０２４年４月以降日本に居住予定の者。
＊なお、上記ア、イ共に東京都およびその周辺に保護者（代理可）が居住、 または居住予定の者に限ります。
受験の際の持ち物は
一次試験：受験票・筆記用具（鉛筆・シャープペンシル・消しゴム）。
二次試験：受験証・体操着・体育館履き・衣服を入れる袋。
計算機および通信機能のついた時計は持ち込みを禁止しています。携帯電話は必ず電源を切って下さい。
教科ごとの足切りはありません。一次試験・二次試験を総合して合否を決定します。
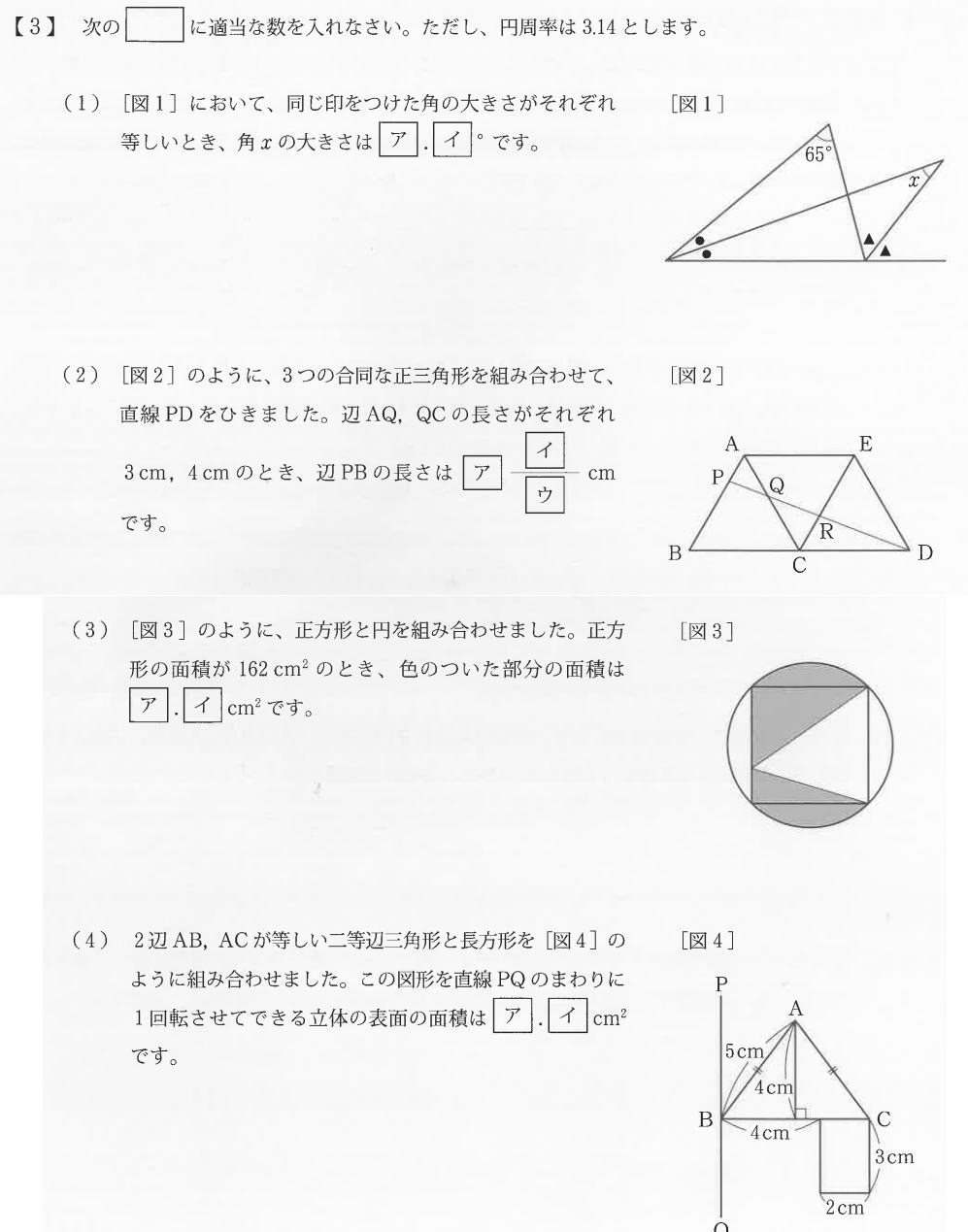
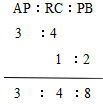
2023年度算数出題内容は1.小問集合(四則計算・比の計算・比の計算・公約数・周期算・場合の数)5問 2.小問集合(食塩水の濃度・流水算・平均算・割合の文章題・公約数の応用)
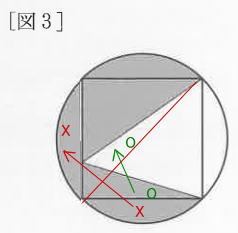
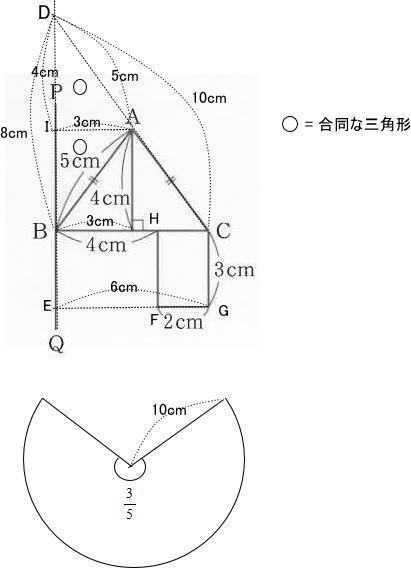
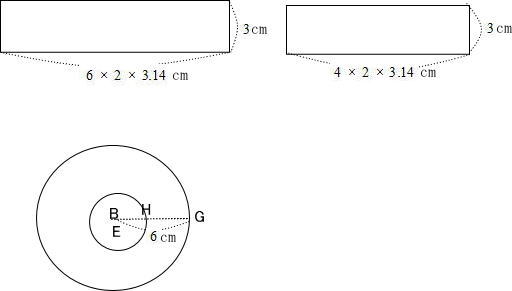
3.平面図形と空間図形4問 4.旅人算 5.水そう算 6.整数の性質 筆算でした。
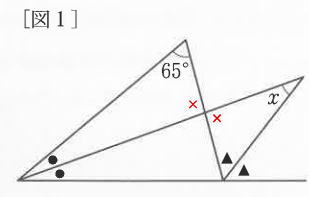
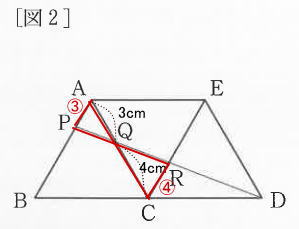
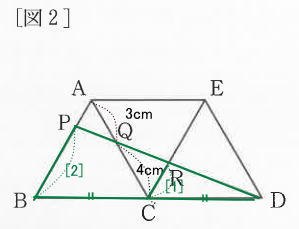
今回は 3.図形問題4問を解説します。
慶應義塾中等部合格のための入試情報と過去問対策へ
