駒場東邦中学・高等学校算数過去問研究
駒場東邦中学校合格のための過去問傾向と対策
駒場東邦中学校・高等学校過去問対策
超難関中学受験指導はスペースONEのプロ家庭教師にお任せください。
駒場東邦中学校2015年度算数入試問題1.(2)平面図形 問題
駒場東邦中学校2015年度算数入試問題1.(2)平面図形 ① 解説解答
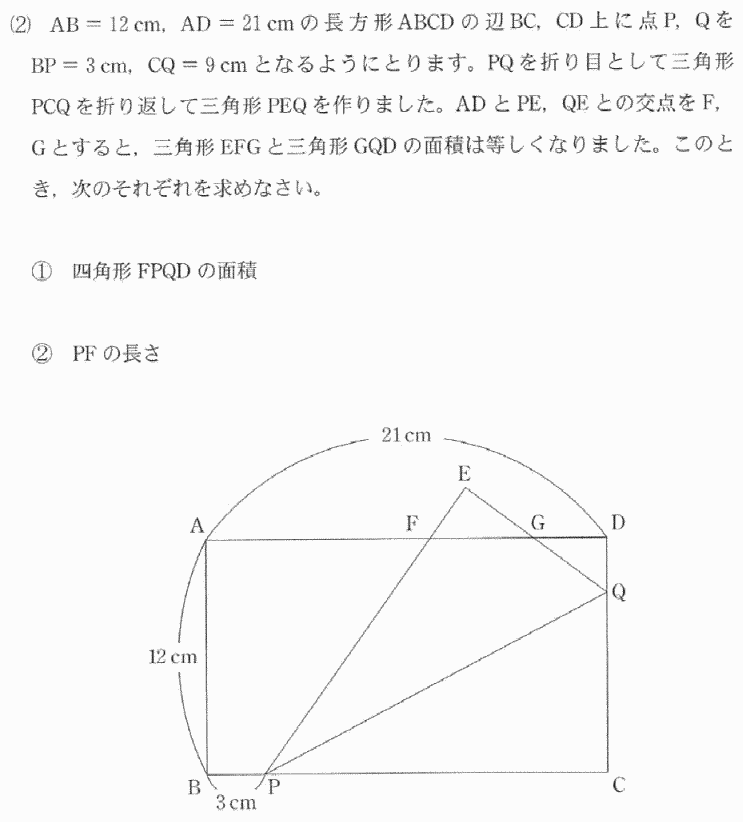
| (2)① 四角形FPQDの面積 |
| 解説 |
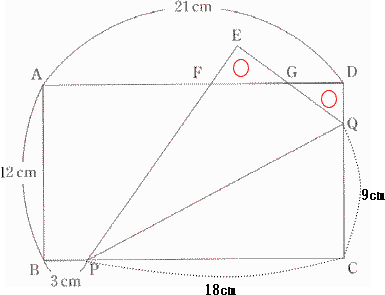 四角形FPQDの面積 = 四角形FPQGの面積 + 三角形GQDの面積 QDの面積 = 三角形EFGの面積なので 四角形FPQDの面積 = 四角形FPQGの面積 + 三角形EFGの面積 = 三角形EPQの面積 三角形EPGQは三角形PCQを折り返してできた三角形なので、 求める面積は 18 × 9 ÷ 2 = 81 |
| 答 81c㎡ |
駒場東邦中学校2015年度算数入試問題1.(2)平面図形 ②解説解答
| (2) ② PFの長さ |
| 解説 |
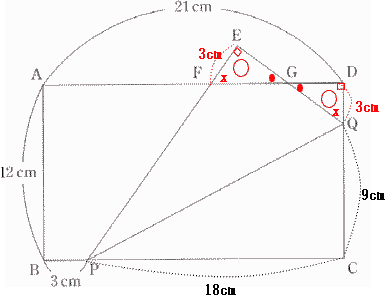 三角形EFGと三角形DQGは 角FGE = 角QGD（対頂角), 角GEF = 角GDQ = 90°であり、, 三角形EFGと三角形GQDの面積は等しいので、三角形EFGと三角形GQDは合同な三角形。 したがって 対応する辺は等しいので EF = DQ PF = PE - EF = PC - DQ = 18 - 3 = 15 |
| 答 15cm |
プロ家庭教師集団スペースONEの駒場東邦中学合格のための過去問対策へプロ家庭教師集団スペースONEの中学受験過去問対策へ