駒場東邦中学・高等学校算数過去問研究
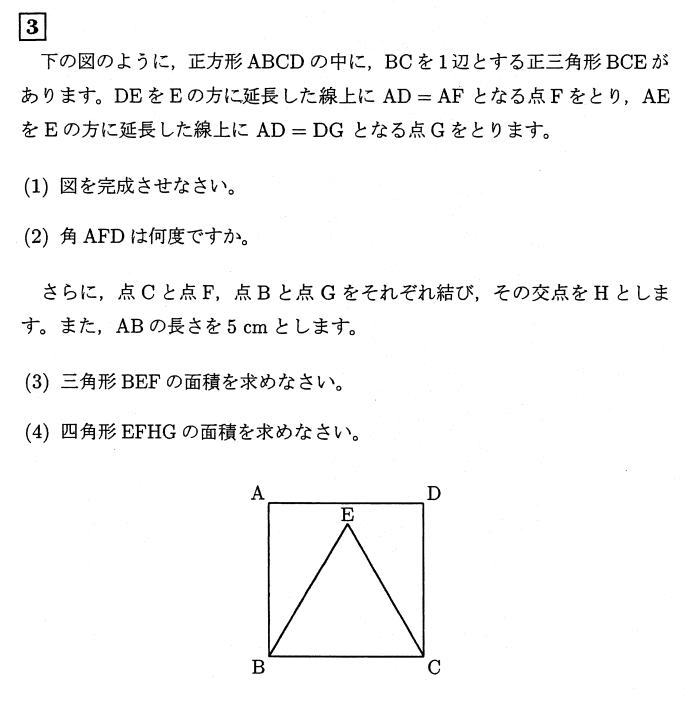
2008年度の駒場東邦中学の平面図形問題は最難関校の入試問題らしく三角形・四角形に関する理解の有無が正答にたどり着けるか否かに分かれる良問でした。
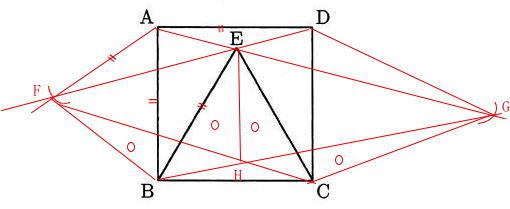
算数入試問題(平面図形にチャレンジ)
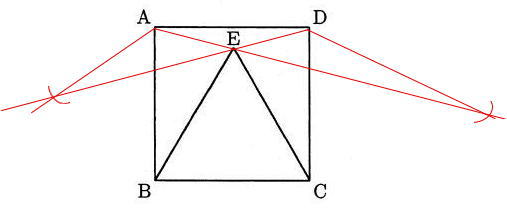
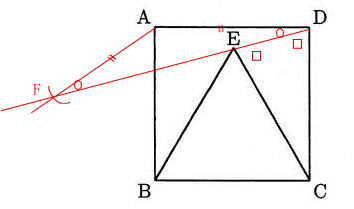
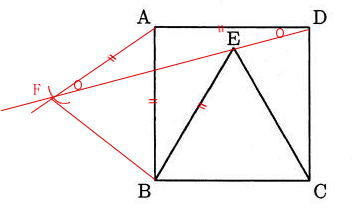
平面図形は駒場東邦中学校算数入試の頻出問題です。特に今回取り上げた作図は進学塾での学習でも余り時間をとって学習することのない問題ですから、自習で補いましょう。
電話: 03-4363-5472
090-3432-2593
受付時間: 平日 AM 10:00 〜 PM 9:00


2008年度の駒場東邦中学の平面図形問題は最難関校の入試問題らしく三角形・四角形に関する理解の有無が正答にたどり着けるか否かに分かれる良問でした。
算数入試問題(平面図形にチャレンジ)
平面図形は駒場東邦中学校算数入試の頻出問題です。特に今回取り上げた作図は進学塾での学習でも余り時間をとって学習することのない問題ですから、自習で補いましょう。