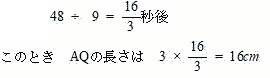弘学館中学校過去問研究
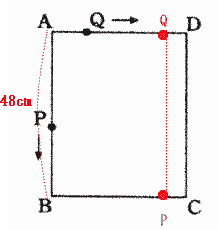
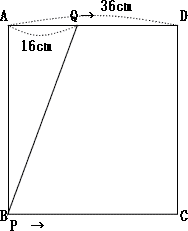
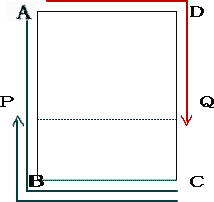
2017年度 弘学館中学校算数入試問題は1.小問集合 2.旅人算 3.食塩の濃度 4.平面上の点移動 5.規則性 が出題されました。
今回は スペースＯＮＥ福岡校のプロ家庭教師が4.平面上の点移動を解説します。速さの追いかけ算の応用問題です。
算数入試問題 平面上の点移動にチャレンジ
弘学館中学校合格のための過去問対策
弘学館中学校・高等学校過去問対策
中学受験指導はスペースONEのプロ家庭教師にお任せください。
弘学館中学校2017年度算数入試問題4.平面上の点移動 問題
弘学館中学校2017年度算数入試問題4.平面上の点移動 (1) 解説解答
解説解答
PQを結ぶ線がはじめて、辺ABに平行になるのは AQ = BPとなるとき、
よってAB 48cmをPがQより余分に進めばよいので、48÷(9 - 3) = 8
答え 8秒後
弘学館中学校2017年度算数入試問題4.平面上の点移動 (2)解説解答
(2) 点Ｑが辺ＡＤ上にあり、台形ＡＢＰＱの面積と台形ＤＣＰＱの面積の比がはじめて、５：１になるのは何秒後ですか。
解説解答
長方形ABCDの横の長さの和が36×2 = 72cmなので、台形ＡＢＰＱの面積と台形ＤＣＰＱの面積の比がはじめて、５：１になるのは
点PがBにつくのは出発して
点Qは1秒ごとに3cm，点Pは1秒ごとに9cmずつ長くなるので、AQ + BP = 60cmとなるのは 出発して
答 9秒後
弘学館中学校2017年度算数入試問題4.平面上の点移動 (3)解説解答
解説解答
点ＰはＡ→Ｂ→Ｃ→Ｂ→Ａに戻る途中，点ＱはＡ→Ｄ→Ｃにいく途中。図の通りＰＱあわせて48×2 + 36×3 = 204cm進んだときなので、
204÷(9 + 3) = 17
答 17秒後