攻玉社中学校・高等学校過去問対策

難関中学受験指導はスペースONEのプロ家庭教師にお任せください。

攻玉社中学校国際学級合格のための過去問対策

男生徒

攻玉社中学校一般学級過去問研究

2011年度攻玉社中学校一般学級算数第１回入試問題は　１．四則計算3問を含む小問４問　２．規則性（暦と割合）　３．旅人算グラフ（動く歩道）　４．平面図形　相似形　５．立体図形　の大問５題構成で、出題内容・問題構成ともに例年通りでした。

2011年度第１回一般学級算数受験者平均点は45.2点　合格者平均点は59.5点。　

昨年度より算数・国語共に大幅に問題が難化し、昨年４科合計合格最低点186点が　2011年度は170点と低い結果になりました。

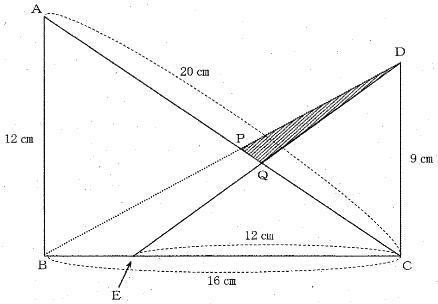
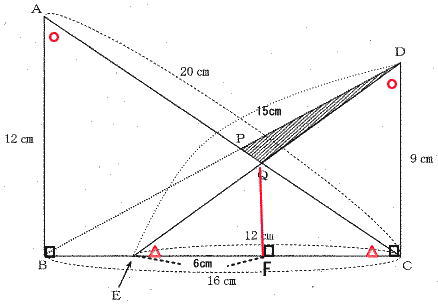
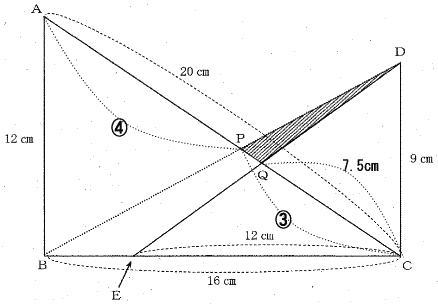
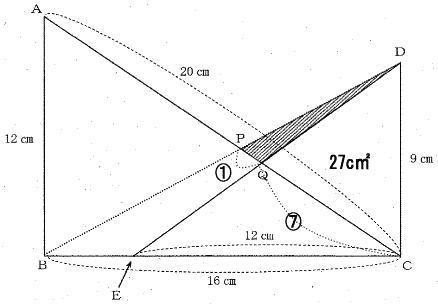
今回は　4．相似形を解説します。

算数入試問題（平面図形；相似形にチャレンジ）

攻玉社中学2011年度算数入試問題4.平面図形　問題


攻玉社中学2011年度算数入試問題4.平面図形(1)解説解答


(1)　辺ＤＥの長さを求めなさい。

解説解答



直角三角形ＡＢＣと直角三角形ＤＣＥは相似形なので、、辺の比（相似比）は１２：９＝４：３

よって　ＡＣ：ＤＥ＝４：３　　　

ＡＣ＝２０ｃｍなので、　　ＤＥ＝２０÷４×３＝１５


答　　　　１５ｃｍ
　　　

攻玉社中学2011年度算数入試問題4.平面図形　(2)解説解答


(2)　三角形ＱＥＣについて、次のものを求めなさい。
①　周囲の長さを求めなさい。

②　面積


①　解説解答



直角三角形ＡＢＣと直角三角形ＤＣＥは相似形なので、対応する角度はそれぞれ等しいから、等しい角度は図の通り。

よって三角形ＱＥＣは二等辺三角形なので、辺ＱＥ＝辺ＱＣ

点Ｑから辺ＥＣに垂線をおろし、その交点をＦとする。

三角形ＱＥＦと三角形ＤＥＣは相似形である。

ＥＦ：ＥＣ＝６：１２＝１：２　なので、相似比は１：２。

(1)より　ＤＥ＝１５ｃｍ　なので、　ＥＱ＝ＣＱ＝１５÷２＝７．５ｃｍ

三角形ＱＥＣの周囲の長さは　ＥＱ＋ＣＱ＋ＥＣ＝１５＋１２＝２７ｃｍ


②　解説①よりＥＱ：ＱＤ＝１：１

よって　三角形ＥＱＣ：三角形ＱＣＤ＝１：１　なので　三角形ＥＱＣの面積は三角形ＥＣＤの面積の1/2.

三角形ＥQＣの面積は　１２×９÷２÷２＝２７ｃ㎡


答　　①　　２７ｃｍ　　　　②　　２７ｃ㎡

攻玉社中学2011年度算数入試問題4.平面図形(3)解説解答


(3)　AP ： PQ ： QCを求めなさい。

解説解答



(2)①より　CQ＝７．５ｃｍ

三角形ABPと三角形CDPは相似形。

AB：CD＝１２：９＝４：３なので、PA：CP＝４：３　　

よって

APの長さは　２０÷７×４＝80/7

CPの長さは　２０÷（３＋４）÷３＝60/7

AP : CQ : QP = 80/7 : 60/7 - 7.5 : 7.5 = 32:3:21

答　　　３２：３：２１

攻玉社中学2011年度算数入試問題4.平面図形　(4)解説解答


(4)　三角形DPQの面積を求めなさい。

解説解答



（３）より　QP：CQ＝３：２１＝１：７　なので

三角形DPQ：三角形DQC＝１：７

（２）②から　三角形DQC＝三角形EQCの面積は２７ｃ㎡

よって三角形DPQの面積は　２７÷７＝27/7ｃ㎡


答　　　27/7 ｃ㎡


Copyright(c) 2013 Sample Inc. All Rights Reserved. Design by http://f-tpl.com