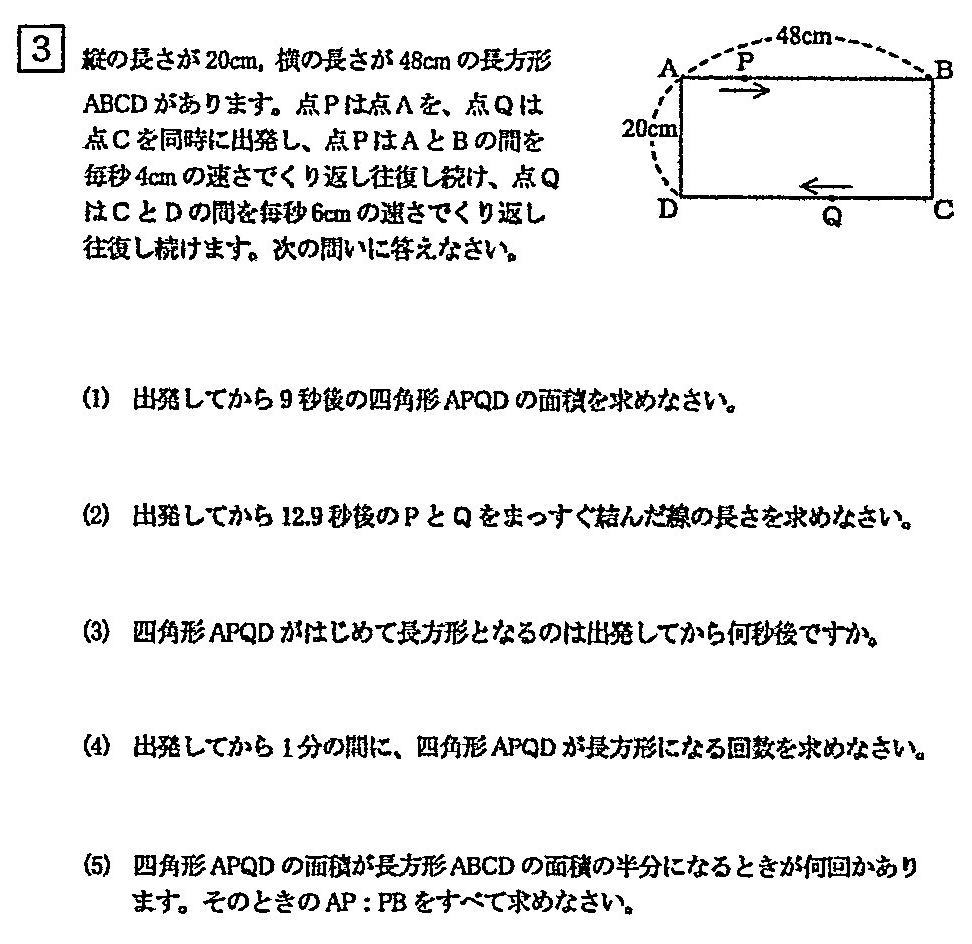
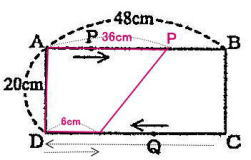
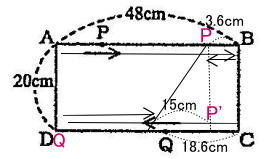
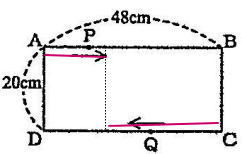
攻玉社中学校一般学級過去問研究
2021年度攻玉社中学校一般学級入学試験は2021年2月1日に実施され、募集人数100名に対し、志願者393名 受験者363名 合格者163名 合格最低点201点。
科目別平均点は 国語受験者平均点70.1点 合格者平均点78.0点 算数受験者平均点58.4点 合格者平均点67.7点 社会受験者平均点32.5点 合格者平均点36.0点 理科受験者平均点34.0点 合格者平均点37.2点でした。
特待生制度では第１回入試上位10名、第２回入試上位10名を特待生とし、入学金および１年次の授業料を免除します。なお、入学後も継続して成績上位の者は、中学２年生まで授業料免除とします。 中学３年生以降は、一般学級・国際学級を合わせた中から新たに選考します。
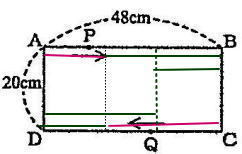
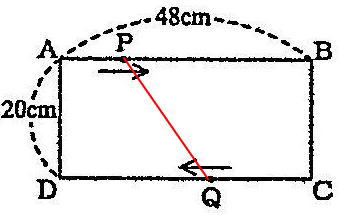
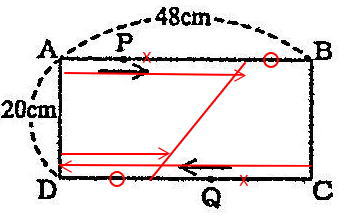
算数第1回入試問題は １．四則計算2問を含む小問3問 ２．小問集合7問 ３．平面上の点移動 ４．立体図形 の大問4題構成で、出題内容・問題構成ともに例年通りでした。
今回は、平面上の点移動を解説します。
プロ家庭教師集団スペースONEの攻玉社中学合格のための過去問対策へ