中学受験指導専門プロ家庭教師の中学受験過去問研究

中学校受験指導はスペースＯＮＥのプロ家庭教師にお任せください。

	ご依頼専用ダイヤル	0120-604-405
	お問い合わせ	03-6868-6040
	お問い合わせメール
	ws-spaceone

HOME

ラ・サール中学校2015年度入試問題(過去問)解答解説

ラ・サール中学校算数過去問研究

2015年度ラ・サール中学校算数入試問題は　例年通り四則計算，小問集合，大問の出題構成でした。解答も例年通り　途中式のない答えのみを解答欄に書き込む形式でした。

今回は2.　小問集合を解説します。

問題2.小問集合にチャレンジ

問題

スペースＯＮＥプロ家庭教師の解説・解答でラサール中学校の発表ではありません。

(1) 　解説解答　

解説 どれをかけても整数となる分数の分母は　7と21と35の最大公約数 すだれ算より　分母は7 どれをかけても整数となる分数の分子は　9と10と6の最小公倍数 すだれ算より分母は　3×2×3×5×1 = 90

（2）解説解答　

解説 Ａ中学校の生徒数を(15)，Ｂ中学校の生徒数を(16)とする。

（3）解説解答　

(3)　Ａ，Ｂ，Ｃ３人の体重の和は164kgです。また、ＡとＢの体重の和はＣの体重の４倍より2kg少なく、Ａの体重はＣの体重の2倍より5.8kg多いです。Ａ，Ｂ，Ｃの体重はそれぞれ何kgですか。 解説 ＡとＢの体重の和はＣの体重の４倍より2kg少なく３人の体重の和は164kgなので、 Ｃの体重は　(164 + 2)÷(1 + 4) = 33.2kg Ａの体重はＣの体重の2倍より5.8kg多いので、33.2 ×2 + 5.8 = 72.2kg・・・Ａの体重 ＡとＢの体重の和は　164 - 33.2 = 130.8kgなので、　130.8 - 72.2 = 58.6kg・・・Ｂの体重 答　　Ａ　72.2kg，　Ｂ 58.6kg，　Ｃ　33.2kg

（4）解説解答　

(4)　右図は長方形を2回折ってできた図形です。χを求めなさい。 解説 折り返す前と折り返した後にできる図形は合同なので、角度も同じ。同じ角度の部分に○，χを付けると図の通り。 ○ = (90 - 54)÷2 = 18 ○ + □ = 134　　なので、　18 + □ = 134　　　□ = 134 - 18 = 116 したがって　χ = (180 - 116) ÷ 2 = 32 答　　　32°

（5）解説解答　

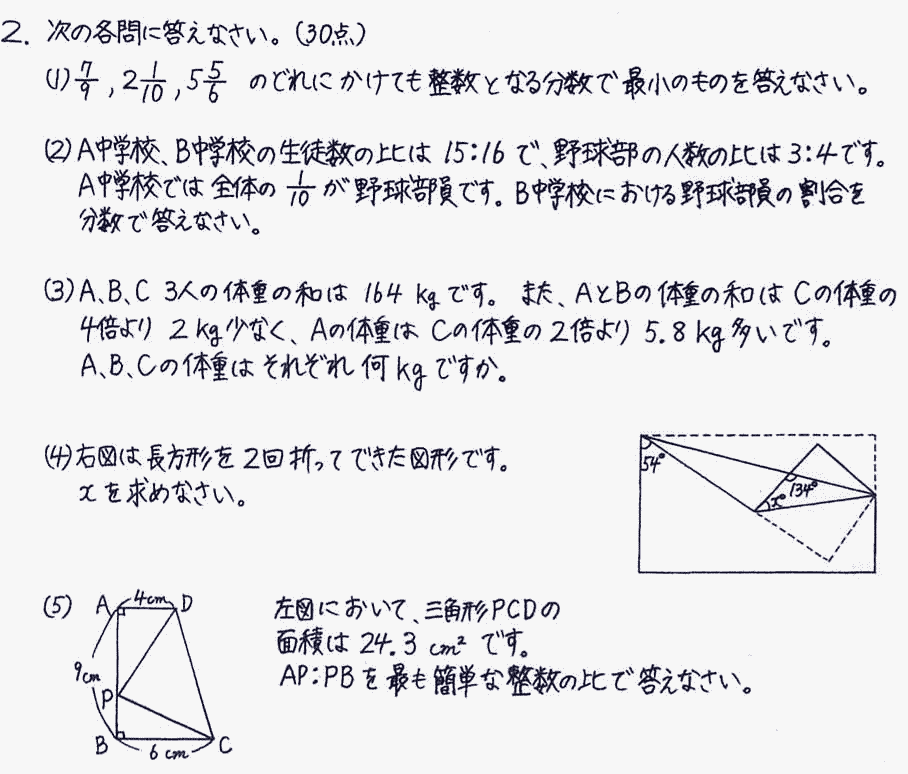
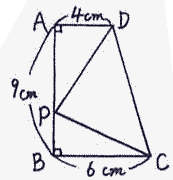
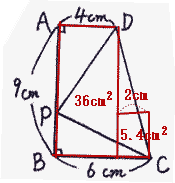
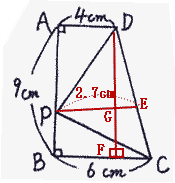
左図において、三角形PCDの面積は24.3c㎡です。AP：PBを最も簡単な整数の比で答えなさい。 解説 点Pから辺DCに、辺BCと平行な直線を引きその交点をEとし、Dから辺BCに垂線をおろしその交点をFとする。 また、PEとの交点をGとする。 △DPCの面積は PE×DF÷2なので、 PE×9÷2 = 24.3 PE = 5.4 PG = 4なので、GE = 5.4 - 4 = 1.4 三角形DGEと三角形PFCは相似形なので、GE：FC = DG：DF GE：FC = 1.4：2 = 7：10 よって　DG：GF = 7：10 - 7 = 3 したがって　AP：PB = 7：3 答　　7：3 別解 台形ABCDの面積は　(4 + 6)×9÷2 = 45c㎡ 三角形PCDの面積は24.3c㎡なので、三角形APDの面積と三角形BPCの面積の和は　45 - 24.3 = 20.7 よって　三角形APDの面積と三角形BPCの面積をそれぞれ2倍して、下図のように長方形をつくると、 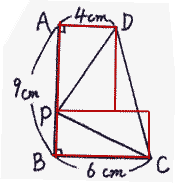その面積の和は20.7×2 = 41.4c㎡ 鶴亀算により、(41.4 - 4×9)÷2 = 2.7・・・PCの長さ よって　APの長さは　9 - 2.7 = 6.3 AP：PB = 6.3：2.7 = 7：3 答　　7：3

ラサール中学校過去問研究ＴＯＰに戻る

中学受験過去問研究ＴＯＰ

プロ家庭教師集団スペースＯＮＥリンク集

高校受験過去問研究

大学受験過去問研究

医学部受験過去問研究

医科大学・医学部入試情報

ＨＯＭＥ

このホームページのすべての文章の文責および著作権はプロ家庭教師集団スペース ONEに属します。