中学受験から医学部受験までプロ家庭教師にお任せください。

明治中学校算数過去問研究

2009年度明治学院中学校第１回算数入試問題は　１．計算を含む小問集合１０問　２．数の性質（トーナメント戦）　３．３人の旅人算　４．円柱の容積　５．規則性（立方体を積み重ねる）　６．数の性質　大問６題構成でした。

合格者最低点　２科目男子114点　女子129点　４科目男子169点　女子185点でした。

算数入試問題（数の性質にチャレンジ）

１辺1cmのマス目でできた表があります。２個のサイコロを４回振るとき, 次のルールでマス目を囲みます。
ルール
①２個のサイコロを振り, 出た目の数の合計をポイントとします。
（例：１と５の目が出たら, ６ポイント）
②２個とも同じ目が出たときは, 出た目を合計せずに, 目の数をポイントとします。
（例：４と４の目が出たら, ４ポイント）
③表は横にサイコロを振った回数, 縦をポイントとします。
④表の縦の１マスは２ポイントを表します。２ポイントで１マスを囲み,
１ポイントでは１マスの半分を斜めに囲みます。
したがって, ３ポイントでは, １マスと半分を囲みます。
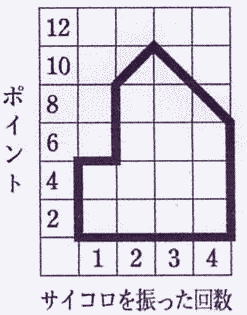
⑤マス目を囲むとき, 囲ってできる多角形の角数が最も小さくなるように囲みます。例：１回目のサイコロの出た目の合計が４,

２回目のサイコロの出た目の合計が９,

３回目のサイコロの出た目の合計が９,

４回目のサイコロの出た目の合計が７のとき, 右表のようにマス目が囲まれます。



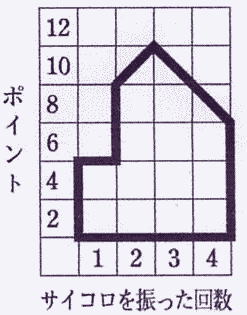
このとき, 次の問いに答えなさい。
(１) 例の表の囲まれた部分の面積を求めなさい。
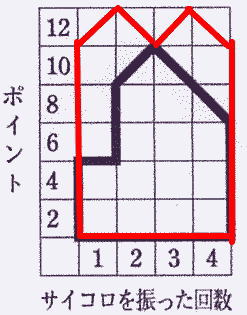
(２) 囲まれた面積が最も大きくなるとき, その面積を求めなさい。
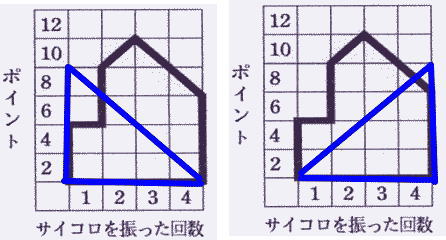
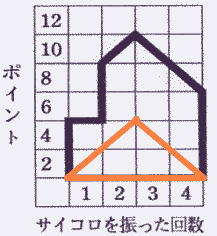
(３) 囲まれた図形が直角二等辺三角形となる場合で, ポイントの合計が最も小さくなるときと, 最も大きくなるときの値を, それぞれ求めなさい。