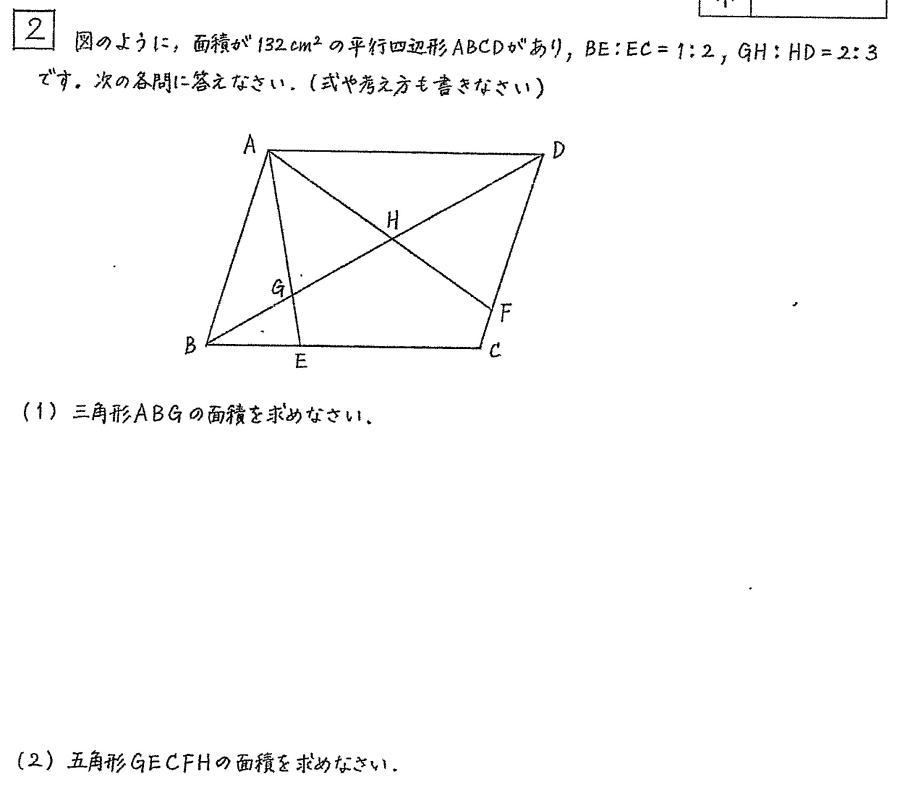
武蔵中学校過去問対策
2022年度武蔵中学校入学試験は2月1日に実施され、募集人数160名に対し、応募者数640名(前年比+56名),受験者数626名(前年比+52名)，合格者数178名(前年比
-5名)，合格最低点202点(前年比+15点)でした。
科目別得点状況は、国語配点100点，合格者平均点67.7点，受験者平均点61.5点 算数配点100点，合格者平均点70.9点 受験者平均点51.4点，理科配点60点，合格者平均点43.7点 受験者平均点39.3点，社会配点60点，合格者平均点35.7点 受験者平均点33.3点でした。
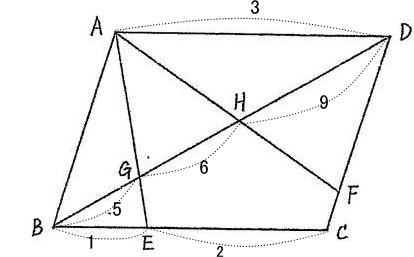
算数入試問題は、例年通りの出題構成でしたが、[1]の四則計算が無くなり，1.整数の性質 2.つるかめ算，[2]平面図形，[3]つり合いと場合の数，[4]速さの問題が出題されました。
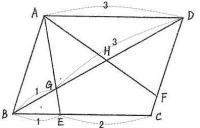
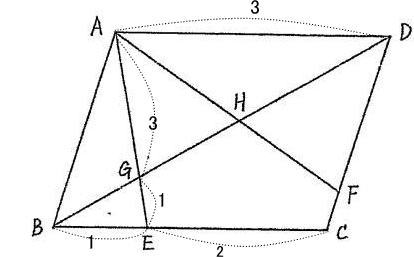
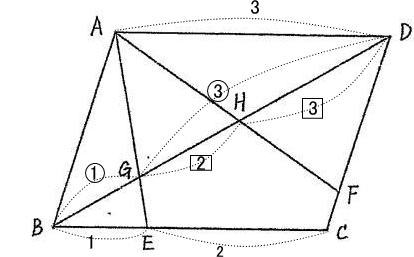
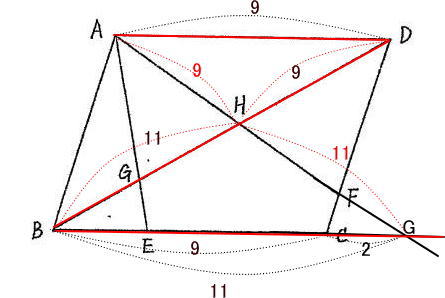
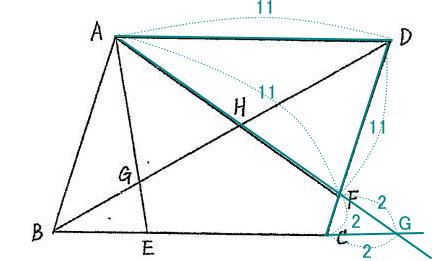
今回は 2.平面図形を解説します。平行四辺形の性質と相似形を用いて解きましょう。
武蔵中学受験指導はスペースONEのプロ家庭教師にお任せください。
プロ家庭教師集団スペースONEの武蔵中学合格のための過去問対策へ