青雲中学校過去問研究
青雲中学校合格のための過去問傾向と対策
青雲中学校過去問対策
中学受験指導はスペースONEのプロ家庭教師にお任せください。
青雲中学校2015年度算数問題3.平面図形 問題
青雲中学校2015年度算数問題3.平面図形(1)解説解答
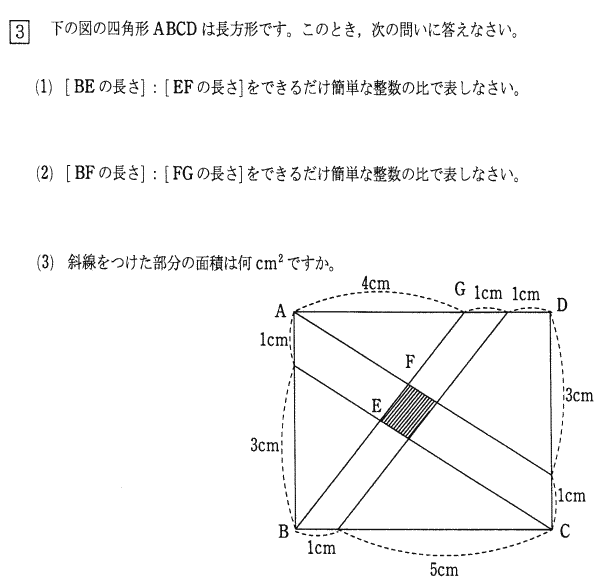
| (1) [BEの長さ]：[EFの長さ]をできるだけ簡単な整数の比で表しなさい。 | ||
| 解答 | ||
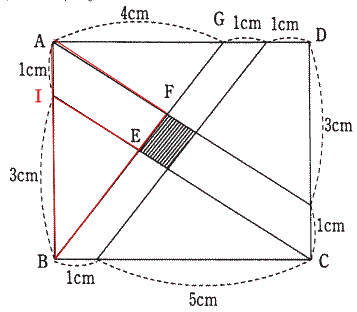
| 右図の通りAB上にAI = 1cm， IB = 3cmとなる点をIとする。 三角形BEIと三角形BFAは相似形なので、BI：IA = 3：1 したがって BE：EF = 3：1 |
 |
|
| 答 3：1 | ||
青雲中学校2015年度算数問題3.平面図形(2)解説解答
| (2) [BFの長さ]：[FGの長さ]をできるだけ簡単な整数の比で表しなさい。 | |
| 解説 | |
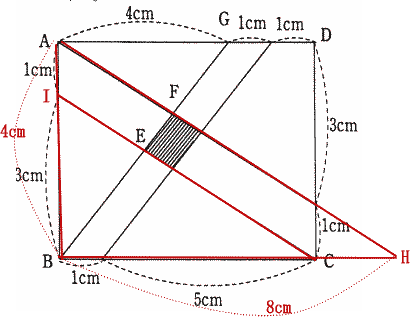
| 右図の通りBCの延長とAFの延長との交点をHとおく。 三角形IBCと三角形ABHは相似形なので、IB：BC = 3：6 = 1：2より、AB：BH = 1：2 AB = 4cmなので、BH = 8cm |
 |
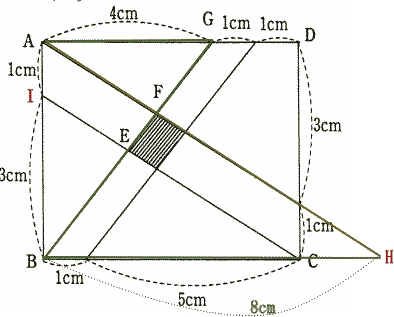
| また 三角形BHFと三角形GAFも相似形。 BH：AG = 8：4 = 2：1 したがって[BFの長さ]：[FGの長さ] = 2：1 |
 |
| 答 [BFの長さ]：[FGの長さ] = 2：1 |
青雲中学校2015年度算数問題3.平面図形(3)解説解答
| (3) 斜線をつけた部分の面積は何c㎡ですか。 | |
| 解説 | |
| (1)，(2)より、BE：EF = 3：1 BF：FG = 2：1 = 4：2 よって BE：EF：FG = 3：1：2・・・① 図のように点J，K，L，Mをおく。 三角形JKCと三角形JJHは相似形なので、JC：CH = JK：KL = 5：2 |
 |
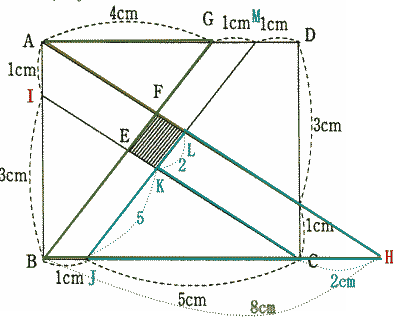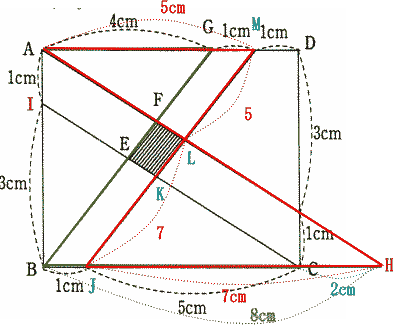
三角形JHLと三角形MALは相似形なので JH：MA = JL：LM = 7：5 よって JK：KL：LM = 5：2：5・・・② BG = JMより ①，②の比の和をそろえる。 BE：EF：FG = 6：2：4 JK：KL：LM = 5：2：5 四角形BGMJは平行四辺形なので 四角形BGMJの面積は 1×4 = 4c㎡ 3つの台形の面積比は 台形BJKE：台形EKLM：台形FLMG = 6 + 5：2 + 2：4 + 5 = 11：4：9 したがって 斜線部台形EKLMの面積は  |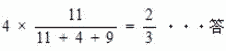
 |