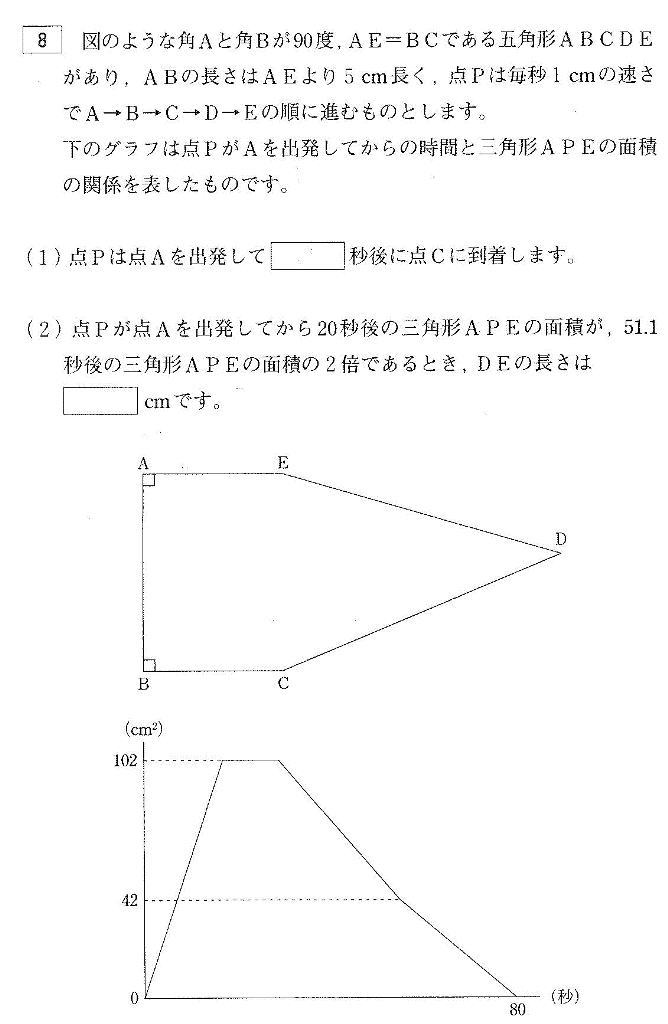
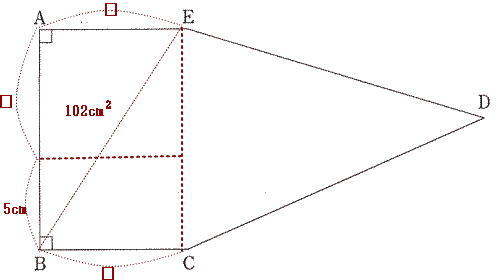
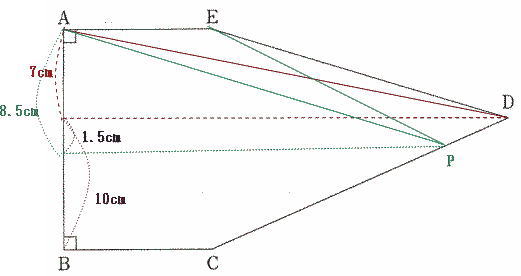
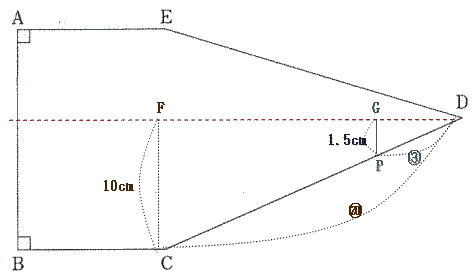
芝中学校過去問傾向と対策
2014年度芝中学校第１回算数入試問題は 例年通りの出題構成で １．計算２問 ２．～１０． 一行問題・大問の組み合わせでした。
解答形式も例年通り 答のみを解答欄に書く形式でした。
2014年度第１回の算数最高点 94点 合格者平均69.3点 受験者平均は52.0点 でした。
芝中学校合格のための過去問傾向と対策
芝中学校・高等学校過去問対策
超難関中学受験指導はスペースONEのプロ家庭教師にお任せください。
芝中学校2014年度算数入試問題8.流水算 平面上の点移動 問題
芝中学校2014年度算数入試問題8.流水算 平面上の点移動 (1)解説解答
解説解答
グラフより 点Pが辺BC上を移動する間、三角形APEの面積は102c㎡
よって 長方形ABCEの面積は204c㎡
AE = BC = □ｃｍとすると、AB = (□ + 5)cm
長方形ABCEの面積は □×(□ + 5) = □×□ + □×5 = 204
10×10 = 100 より □に11から適する数字を探すまで当てはめていくと、
12×12 + 12×5 = 204
したがって、AB = BC = 12cm, AB = 12 + 5 = 17cm
点Pが点Aを出発して、点Cに到着するまでに動く距離は 17 + 12 = 29cm
点Pの速さは秒速1cmなので、点Cに到着するのは 29秒後
答 29秒後
芝中学校2014年度算数入試問題8.流水算 平面上の点移動 (2)解説解答
(2) 点Pが点Aを出発してから20秒後の三角形APEの面積が、51.1秒後の三角形APEの面積の２倍であるとき、DEの長さは□cmです。
解説解答
グラフより点Pが点Dに到着したときの三角形APEの面積は42c㎡，
AEを底辺としたときの三角形の高さは 42×2÷12 = 7cm。
また点Pが点Aを出発してから20秒後は点Pがは辺BC上にあり、点Cを通過して 51.1 - 29 = 22.1秒後の三角形APEの面積の２倍であるので、
点Pが辺BC上にあるときと、51.1秒後の高さの比は2：1より、
51.1秒後のAEを底辺としたときの三角形の高さは 17÷2 = 8.5cm。
点Dから辺ABに垂線をおろし、また、その直線に点C，51.1秒後の点Pの位置から垂線をおろし、その交点をそれぞれ点F，点Gとすると、図の通り
三角形DGPと三角形DFCは相似形、相似比は1.5：10 = 3：20
⑳ - ③ = ⑰ = 51.1 - 29 = 22.1cm
したがって CDの長さ⑳は
22.1÷17×20 = 26cm
点Pが点Aを出発して点Dに到着するのに進む距離は 29 + 26 = 55cm
グラフより 点Pが点Eに到着するのは出発後80秒なので、80cm
よって DEの長さは 80 - 55 = 25cm
答 25cm