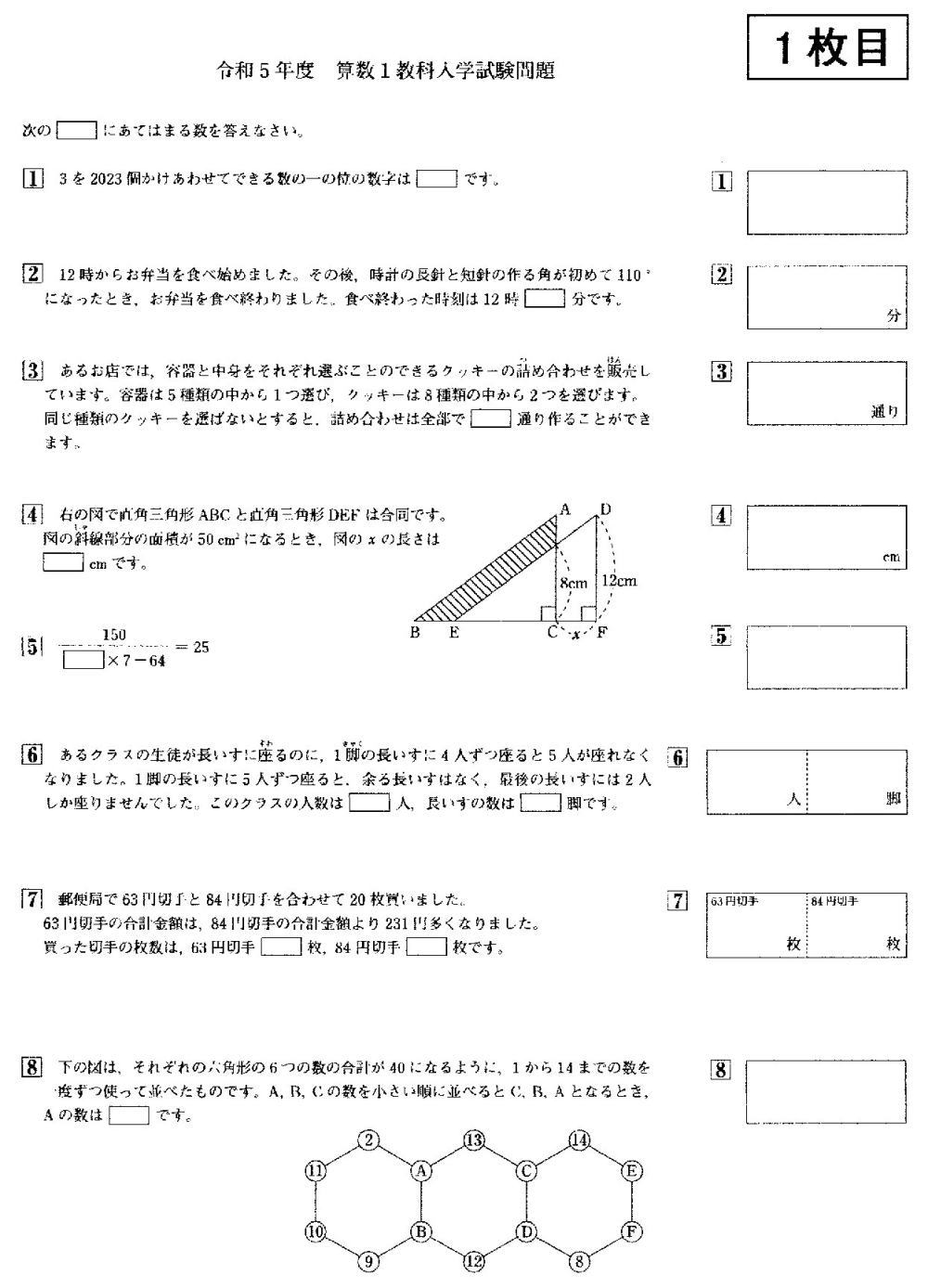
品川女子学院中等部過去問対策

中学受験指導はスペースONEのプロ家庭教師にお任せください。

品川女子学院中等部合格のための過去問対策

girl

品川女子学院中等部算数過去問研究

2023年度品川女子学院中等部算数１科目入試は2月1日午後に実施されました。

男子校では算数1科目入試を実施する中学は増えてきましたが、女子校ではまだ珍しく、また午後入試ということもあってチャレンジしやすい入試日程になっています。

2023年度算数1科目入試は募集人数　20名に対し　出願者数320名　受験者数301名　合格者数132名　

配点100点に対し　合格者平均点70.9点　受験者平均点54.5点　合格ライン58点でした。

試験時間は60分。出題形式は　小問集合25問　答えは全て問題文の右側にある解答欄に書き込み、解答欄に書かれているもののみ採点の対象となるので、部分点はありません。

今回は　1枚目の問題8問を解説します。


品川女子学院中等部2023年度算数1科目入試問題1枚目　問題


品川女子学院中等部算数１科目入試問題解説解答


品川女子学院中等部2023年度算数1科目入試問題1枚目　解説解答

[1]　3を2023個かけてできる数の一の位の数字は□です。

解説解答

3をかける回数　　　1個　　　　2個　　　　　3個　　　　　　4個　　　　　5個　　　　　　

一の位の数　　　　　3　　3×3 = 9 　　　9×3 = 27　　　7×3 = 21　　　1×3 = 3

(3，9，7，1)　の4個で1周期になるので、2023 ÷4 = 505 ・・・3

余りの数が3なので　(3，9，7，1)の3番目の数


答　　　　7



[2]　12時からお弁当を食べ始めました。その後、時計の長針と短針の作る角が110°になったとき、お弁当を食べ終わりました。食べ終わった時刻は12時□分です。

解説解答

12時の時に短針と長針のつくる角度は0°。

短針は1分間に　0.5°動き、長針は1分間に6°動くので、1分ごとに 6 - 0.5 = 5.5°角度の差が開く。

よって　角度の差が110°になるのにかかる時間は　110 ÷5.5 = 20分


答　　20


[3]　　あるお店では、容器と中身をそれぞれ選ぶことのできるクッキーの詰め合わせを販売しています。容器は5種類の中から1つ選び、クッキーは8種類の中から2つを選びます。同じ種類のクッキーは選ばないとすると、詰め合わせは全部で□通りつくることができます。

解説解答

箱の選び方は　5通り

クッキーは8種類から2つ選ぶ選び方は　8×7÷2 = 28通り

よって詰め合わせの場合の数は　5×28 = 140


答　　　140通り


[4]　右の図で直角三角形ABCと直角三角形EEFは合同です。図の斜線部分の面積が50c㎡になるとき、図のxの長さは□cmです。

解説解答

図の通り辺ACと辺EDの交点をGとする。

中学受験等積変形

直角三角形ABCと直角三角形EEFは合同なので、直角三角形GEC + 斜線部の面積 = 直角三角形GEC + 台形GCFDの面積

したがって 台形GCFDの面積は　50c㎡

三角形GECと三角形DEFは相似形

GC：DF = EC：EF = 8：12 = 2：3

よって　三角形GECと三角形DEFの面積比は　2×2 ：3×3 = 4：9

台形GCFDの面積 ⑨ - ④ = ⑤ = 50c㎡ なので、△DEFの面積は　50×9/5 = 90c㎡

EFの長さは　EF×12 ÷ 2 = 90　　　EF = 90÷6 = 15cm

CF = 15×1/3 = 5

答　　　5cm


四則演算

解説解答

150 ÷ (□×7 - 64) = 25

　　　 □×7 - 64 　= 150 ÷ 25

　　　　　　□×7　= 6 + 64

　　　　　　　□　 = 70 ÷7 = 10


答　　　10


[6]　あるクラスの生徒が長椅子に座るのに、1脚の長椅子に4人ずつ座ると5人がすわれなくなりました。1脚の長椅子に5人ずつ座ると、余る長椅子はなく、最後の長いすには2人しか座りませんでした。このクラスの人数は□人、長いすの数は□脚です。

解説解答

過不足算の面積図より　縦軸に1脚に座る人数、横軸に長椅子の脚数とする。

中学受験分配算

4人ずつ座ると5人座れない人がいて、5人ずつ座ると、最後の長いすには2人しか座らないので、さらに3人座ることができる。

1脚あたり座る人数の差は 5 - 4 = 1人　人数の差は5 + 3 = 8人

よって　長いすの脚数は　8÷1 = 8

人数は　4×8 + 5 = 37


答　　　このクラスの人数 37人、長いすの数は8脚


[7]　郵便局で63円切手と84円切手を合わせて20枚買いました。63円切手の合計金額は、84円切手の合計金額より231円多くなりました。買った切手の枚数は63円切手□枚、84円切手□枚です。

解説解答

63円切手と84円切手を同数買うと、差額は84円切手が 84 - 63 = 21円多い。

63円切手を84円切手より1枚多く買うと、差額は63円切手が　63 - 21 = 42円多い。

更に63円切手を1枚ずつ多く買うと　42 + 63円多くなっていく。

よって　63円切手の合計金額が84円切手の合計金額より231円多くなるのは

(231 - 42) ÷63 = 3

したがって　63円切手が84円切手より　3 + 1 = 4枚多いときなので

63円切手　(20 + 4) ÷2 = 12枚　　　84円切手　20 - 12 = 8枚


答　　　63円切手　12　　　　84円切手　8枚


[8]　下の図は、それぞれの六角形の6つの数の合計が40になるように、1から14までの数を一度ずつ使って並べたものです。A，B，Cの数を小さい順に並べるとC，B，Aとなるとき、Aの数は□です。

解説解答

中学受験思考力

A + B = 40 - (11 + 10 + 2 + 9) = 8

C + D = 40 - ( 8 + 13 + 12) = 7

E + F = 40 - ( 7 + 22) = 11

1から14までの数のうち　A, B，C，D，E，F に入るのは　1　2　3　4　5　　6　7　8　9　10　11　12　13　14

1，3，4，5，6，7 で、2数の和が　

A + B = 8 になる組み合わせ　(1，7) (3，5)

C + D = 7になる組み合わせ 　(1，6)(3，4)

E + F = 11になる組み合わせ　(4，7)　　1通りのみ

よって　A + B = 8 になる組み合わせ　(1，7) (3，5)　より(3，5)

C + D = 7になる組み合わせ 　(1，6)(3，4)　より (1，6)

C＜B＜A　なので 　c = 1，B = 3，A = 5


答　　　5
Copyright(c) 2013 Sample Inc. All Rights Reserved. Design by http://f-tpl.com