早稲田実業学校中等部算数過去問研究
2008年度早稲田実業学校中等部算数入試問題（流水算にチャレンジ）
早稲田実業学校中等部合格のための過去問対策
早稲田実業学校中等部2008年度算数入試問題 5.流水算 問題
5. 一定の速さで流れている川の上流にＸ地点，その12km上流にＹ地点があり、船Ａ，Ｂは、Ｘ地点を出発し、Ｙ地点に着くと10分休んだ後、Ｘ地点に戻ります。船Ａは、Ｘ地点を出発してから30分後に、あとからＸ地点を出発した船ＢにＰ地点で追い抜かれました。
追い抜いた船Ｂは、Ｙ地点で10分休んだあと、エンジンを止めて川の流れの速さだけでＸ地点に向けて出発しました。
すると、船ＢはＰ地点で船Ａを追い抜いたときから95分後にＹ地点に向かっている船ＡとＱ地点ですれ違いました。
Ｙ地点に着いた船Ａは、10分休んだあと、静水での速さを、行きの静水での速さの半分にして、Ｘ地点に向けて出発しました。
すると、船Ａは、Ｑ地点で船Ｂとすれ違ったときから95分後に、Ｐ地点で船Ｂを追い抜きました。
下のグラフは、船Ａ，Ｂの時間と距離の関係を表したものです。次の各問に答えなさい。
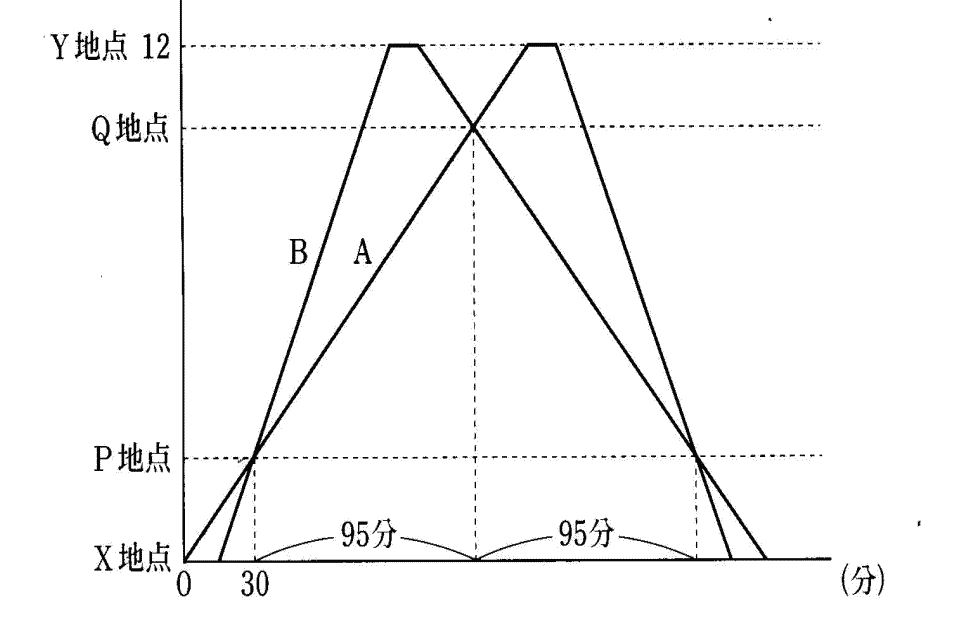
（１）船ＢがＸ地点に戻った時刻は、船ＡがＸ地点を出発してから何分後ですか。
（２）船Ａの、Ｙ地点へ向かうときの静水での速さは、川の流れの速さの何倍ですか。
（３）船Ｂの、Ｙ地点に向かうときの静水での速さは、毎分何ｍですか。
早稲田実業学校中等部2008年度算数入試問題 5.流水算 (1)解説解答
船ＢがＸ地点に戻った時刻は、船ＡがＸ地点を出発してから何分後ですか。
解説
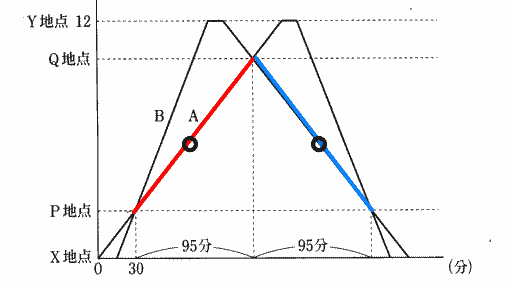
船ＡがＰＱ間を上る時間と船ＢがＱＰ間を下る時間が同じなどで、Ａの上りの速さとＢの下りの速さ（＝川の流れの速さ）が同じ。
よって船ＡがＸＰ間を30分で進んでいるので、船ＢがＰＸ間を川の流れで進むのにも30分かかる。
船ＢがＸ地点に戻る時間は 船Ａが出発して 30＋95×2＋30 = 250
答 250分
早稲田実業学校中等部2008年度算数入試問題 5.流水算 (2)解説解答
解説
川の流れの速さを①にするとＡの上りの速さは
Ａの静水時の速さ - 川の流れの速さ① = 川の流れの速さ① なので
Ａの静水時の速さ = ②
答 ２倍
早稲田実業学校中等部2008年度算数入試問題 5.流水算 (3)解説解答
船Ｂの、Ｙ地点に向かうときの静水での速さは、毎分何ｍですか。
解説
Ａの下りの速さはＡの静水時の速さの1/2＋川の流れの速さ①なので ②÷２＋①＝②
Ａの上りの速さ：下りの速さ＝１：２
よってかかった時間は２：１
ＡはPY間を往復９５×２－１０＝１８０分間で進んでいるので、上りにかかった時間は１８０÷３×２＝１２０分
ＰＹ間を１２０分なので、ＸＹ間１２ｋｍを１２０＋３０＝１５０分で進んだことになる。
よってＡの上りの速さは １２０００÷１５０＝８０ｍ/分
Ａの上りと川の流れの速さは同じなので、川の流れの速さも分速８０ｍ。
またＸＰ間は分速８０ｍで３０分かかる距離なので、８０×３０＝２４００ｍ。
よってＰＹ間は１２０００－２４００＝９６００ｍ
船Ｂは下りは川の流れの速さだけでＰＹ間を進んだので、かかった時間は９６００÷８０＝１２０分
船ＢがＰＹ間を上るのにかかった時間は９５×２－１０ー１２０＝６０分
船ＢがＹ地点に向かうときの速さは ９６００÷６０＝１６０ｍ/分
船Ｂの静水時の速さは １６０＋８０＝２４０ｍ/分
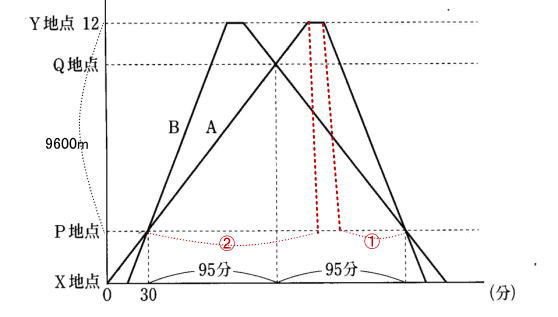
答 ２４０ｍ/分