高輪中学校帰国生過去問研究
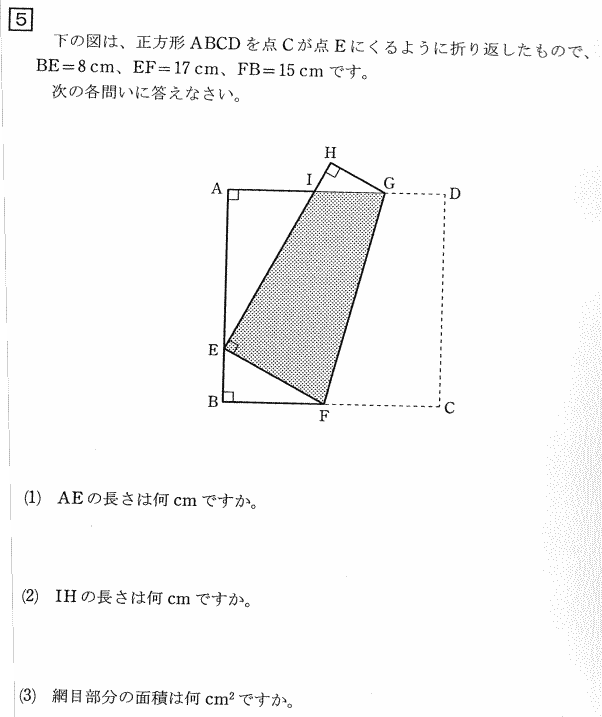
2017年度高輪中学校帰国生算数入試問題は、1.四則計算を含む小問8問,2.小問集合3問 3.文章題 4.旅人算 5.平面図形(正方形の折り返し図形)が出題されました。
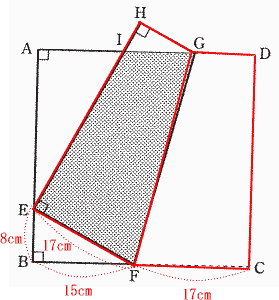
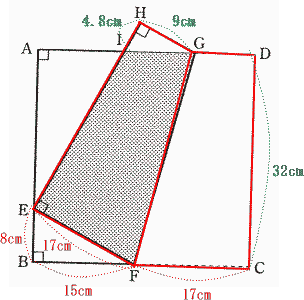
今回は 5.平面図形を解説します。折り返しした図形は合同な図形になることを利用して解きましょう。

中学受験指導はスペースONEのプロ家庭教師にお任せください。

2017年度高輪中学校帰国生算数入試問題は、1.四則計算を含む小問8問,2.小問集合3問 3.文章題 4.旅人算 5.平面図形(正方形の折り返し図形)が出題されました。
今回は 5.平面図形を解説します。折り返しした図形は合同な図形になることを利用して解きましょう。