東邦大学附属東邦中学校算数過去問研究
東邦大学附属東邦中学校後期算数入試問題（音の速さにチャレンジ）
東邦大学付属東邦中学校合格のための過去問傾向と対策
東邦大学付属東邦中学校過去問対策
中学受験指導はスペースONEのプロ家庭教師にお任せください。
東邦大学付属東邦中学校2022年度算数入試問題2.小問集合 問題
図のように船Ａは毎時１８ｋｍの速さで、船Ｂは毎時２８．８ｋｍの速さで向かい合って進んでいます。
船Ａが汽笛を鳴らし、園生とがＢに届くと同時にＢも汽笛を鳴らしました。
Ｂの汽笛はＡが汽笛を鳴らしてから１３．６秒後にＡに届きました。
音は毎秒３４０ｍの速さで伝わるとして、次の（１）（２）に答えなさい。
（２）Ａが汽笛を鳴らしたとき、ＡとＢの間の距離は何ｍでしたか。
東邦大学付属東邦中学校2022年度算数入試問題2.小問集合 (1)約数の問題 解説解答
（１）Ａがならした汽笛の音がＢに届くまで何秒かかりますか。
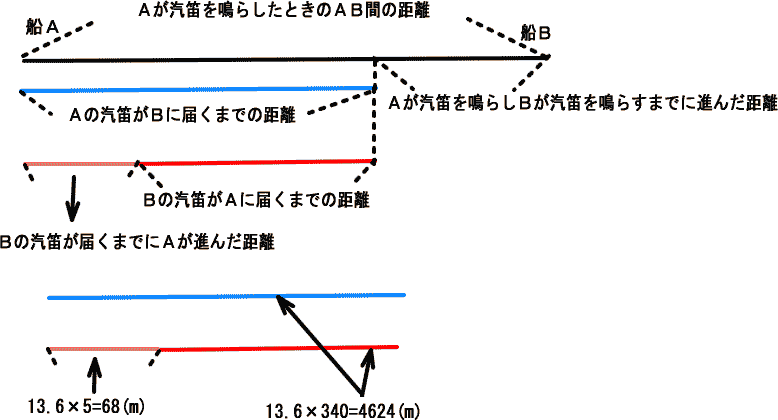
船Ａの時速１８ｋｍ＝18000÷3600=5m/秒 船Ａが汽笛を鳴らして船Ｂに届くまでの距離は （13.6×340＋13.6×5）÷２＝2346
Aが鳴らした汽笛の音がＢに届くまでにかかる時間 2346÷340=6.9(秒)
東邦大学付属東邦中学校2022年度算数入試問題2.小問集合 (2)食塩水の濃度解説解答
（２）Ａが汽笛を鳴らしたとき、ＡとＢの間の距離は何ｍでしたか。
6.9秒後に船Ａの鳴らした汽笛が船Ｂに届く距離になる。船Ｂの秒速は２８８００÷３６００＝８ｍ/秒 ６.９×（３４０＋８）＝２４０１.２ｍ