東邦大学附属東邦中学校過去問研究
算数入試問題注目の一題 方陣算にチャレンジ）
東邦大学付属東邦中学校合格のための過去問傾向と対策
東邦大学付属東邦中学校過去問対策
中学受験指導はスペースONEのプロ家庭教師にお任せください。
東邦大学付属東邦中学校2008年度算数入試問題 方陣算と規則性 問題
図Ⅰのように、3,600枚の硬貨を正方形の形に並べます。次に図Ⅱのように一番外側の１周部分（斜線部）の硬貨を取り除きます。同じようにして、順に外側の硬貨を取り除く操作を、硬貨が４枚残るまで続けます。このとき、つぎの（１）～（３）の問いに答えなさい。
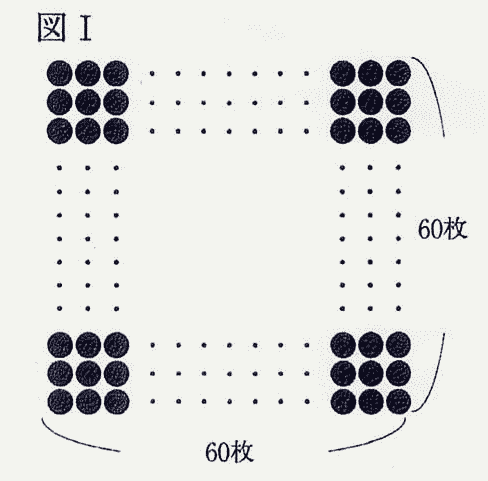
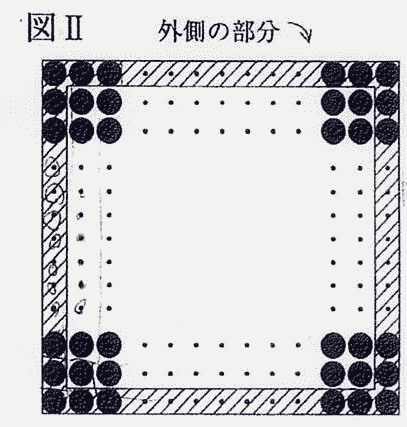
（１） １０回目の操作の後、残った硬貨は何枚ですか
（２） 何回目かの操作の後、それまでに取り除いた硬貨を合計した枚数が、残った硬貨の枚数より初めて多くなりました。何回目の操作の後ですか。
（３） ある１回の操作で取り除いた硬貨を全部使って、正方形の形に並べられる場合があります。はじめに出来るのは６回目ですが、次に正方形の形に並べられるのは何回目ですか。
東邦大学付属東邦中学校2008年度算数入試問題 方陣算と規則性 (1)解説解答
解説解答
図のように １回目に取り除く硬貨の数 （６０－１）×４
このとき残った硬貨の数 （６０－２）×（６０－２）
同様に２回目に取り除く硬貨の数（６０－３）×４
よって 毎回取り除く硬貨の数は６０－１・３・５・７・・・と規則的に続くので、
１０回目に取りのぞく硬貨の数は ２×１０－１＝１９ （６０－１９）×４
このとき残った硬貨の数は ｛６０－（１９＋１）｝×｛６０－（１９＋１）｝＝１６００個
（別解）
１回目に取り除く硬貨の数 ２３６個 ２回目には２２８個・・・と等差が８の数列になるので、
１０回目に取り除く硬貨の数は２３６－８×（１０－１）＝１６４個
等差数列の和より１回目から１０回目までに取り除く硬貨の数は （２３６＋１６４）×１０÷２＝２０００
残った硬貨の数は３６００－２０００＝１６００個
答 １６００個
東邦大学付属東邦中学校2008年度算数入試問題 方陣算と規則性 (2)解説解答
解説
全部で３６００こあるので、３６００÷２＝１８００ 取り除いた硬貨の合計が１８０１個以上になったときの操作になる。１０回目の操作の後で取り除いた硬貨の合計は ２０００個 ９回目までに取り除いた硬貨の合計は ２０００－１６４＝１８３６個 ８回目までに取り除いた硬貨の合計は２０００－１６４×２ー８＝１６６４個 よって９回目の操作の後９回目までに取り除いた硬貨の合計が、残った硬貨の合計より多くなる。
答 ９回目
東邦大学付属東邦中学校2008年度算数入試問題 方陣算と規則性 (3)解説解答
解説
６回目の操作のときに取り除く硬貨の数は ２×６ー１＝１１ （６０－１１）×４＝１９６個 １９６＝１４×１４
次に正方形の形に並べられる硬貨の数は １３×１３，１２×１２，１１×１１・・・となり、取り除く硬貨の数は２３６－８の倍数になる。
これに当てはまるのは１０×１０＝１００ ２３６－１００＝１３６＝１７×８ １回の操作で取り除く硬貨が１００枚のとき、 １７＋１＝１８回目
答 １８回目