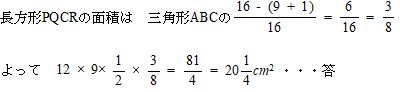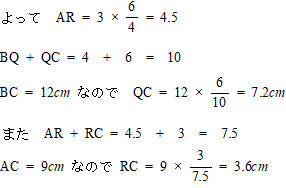東京都市大学等々力中学校帰国生過去問対策
2021年度の東京都市大学等々力中学校帰国生入試は募集人数20名,出願資格は① 現在国内に在住し海外在住1年以上で原則帰国後3年以内 ② 現在海外に在住し令和3年4月1日までの海外在住機関が1年以上の者 です。
受験教科は算数・作文必修,英語・国語選択 面接は個人グループです。
2020年度算数入試問題は 1.四則計算3問 2.小問集合5問 3.平面図形 4.割合 5.流水算 6.場合の数でした。
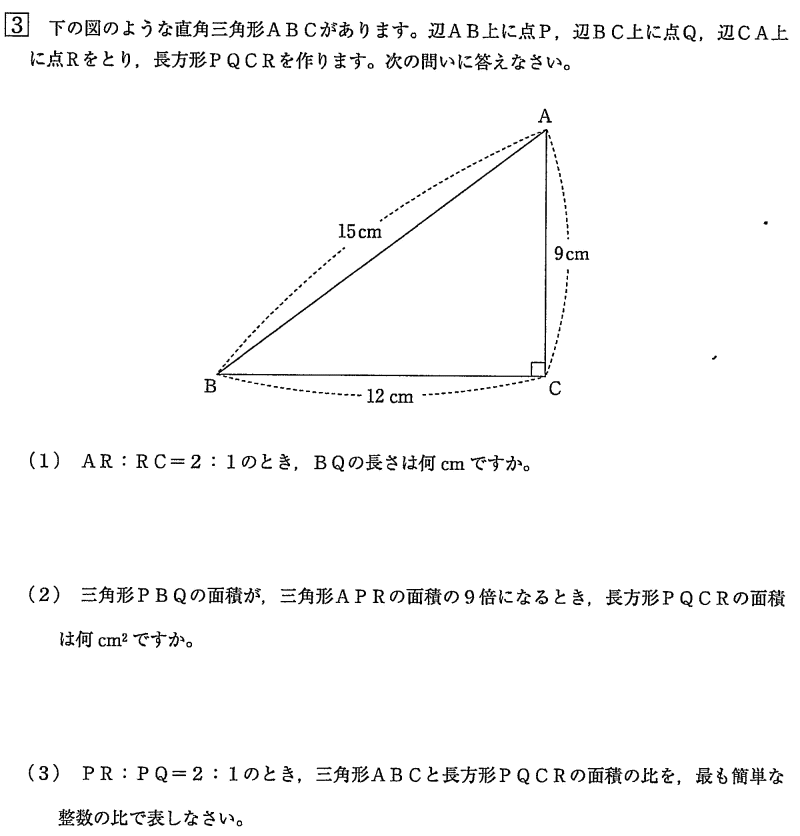
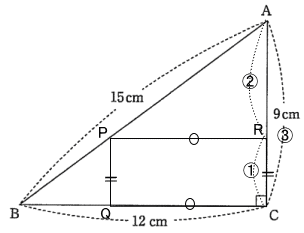
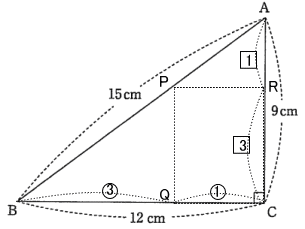
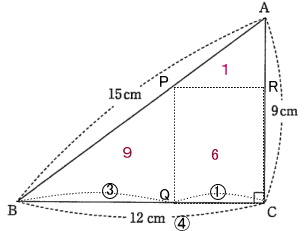
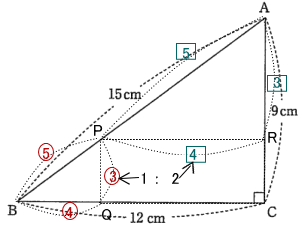
今回は算数入試問題3.平面図形を解説します。相似比と面積比に注意して解きましょう。
スペースONEプロ家庭教師の東京都市大学等々力中学校帰国生入試問題解説解答
| 等々力中学校帰国生入試問題(スペースONEプロ家庭教師算数模範解答)を頒布中です。 | ||
| メールでお問い合わせください。pro.tutor@ws-spaceone.jp 着信拒否設定がなされスペースONEからの返信メールが送れない場合がございます。弊社からの返信メールがない場合(090-3432-2593),skype(ws-spaceone)にお問い合わせください。 |
||
| 模範解答 | ||
| 算数 2024年度・2023年度・2022年度・2021年度 | ||
| 国語 2024年度・2023年度・2022年度 | ||