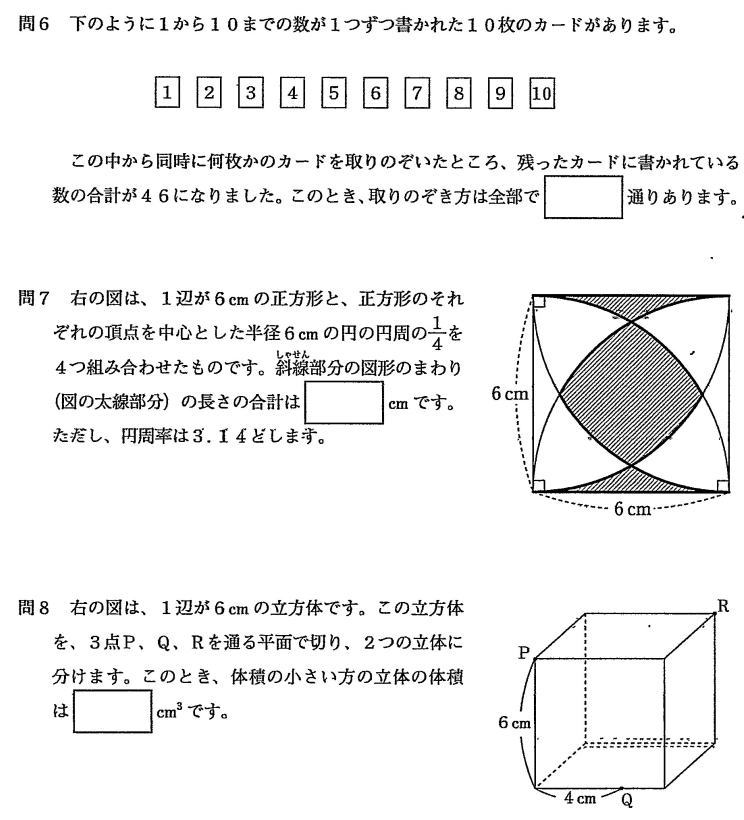
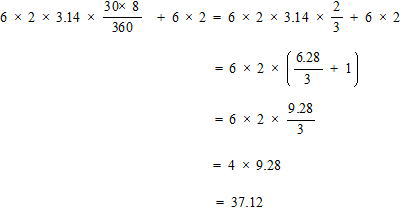帰国子女入試はプロ集団にお任せ/プロ家庭教師集団スペースONEの東京都市大学付属中学2021年度帰国生算数入試問題

東京都市大学附属中学校過去問対策

中学受験指導はスペースONEのプロ家庭教師にお任せください。

東京都市大学附属中学帰国生入試合格のための過去問傾向と対策

東京都市大学付属中学帰国生過去問対策

2021年度東京都市大学付属中学校帰国生入学試験は1月6日に実施されました。

帰国生入試方式はA方式国語型・作文型，B方式2教科式・4教科式ででした。

A方式算数受験者平均点52.2点合格者平均点86.4点，B方式受験者受験者平均点合格者平均点74.8点でした。

帰国生算数入試問題は　1.小問集合83問　2.旅人算　3.平面図形　4.水そうに水を入れる割合の問題　5.場合の数が出題されました。

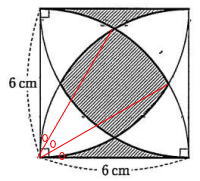
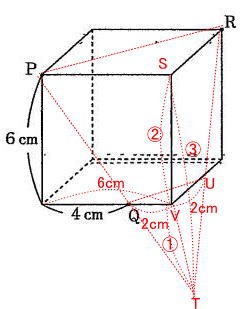
今回は1.小問集合から、受験者平均得点率31%，合格者平均得点率44%の問6 場合の数，受験者平均得点率41%，合格者平均得点率58%の問7 平面図形，受験者平均得点率61%，合格者平均得点率78%の問8 立体図形の切断を解説します。.

東京都市大学付属中学2021年度帰国生算数入試問題1.問6,7,8 　問題

東京都市大学付属中学算数入試問題解説解答

東京都市大学付属中学2021年度帰国生算数入試問題1.問6場合の数　解説解答

問6　下のように1から10までの数が1つずつ書かれた10枚のカードがあります。

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10]

この中から同時に何枚かのカードを取り除いたところ、残ったカードに書かれている数の合計が46になりました。このとき、取りのぞき方は全部で□通りあります。

解説解答

1から10までの数の和は　(1 + 10) ×10÷2 = 55

残ったカードに書かれている数の合計が46なので、取り除いたカードの和は　55 - 46 = 9

合計で　9になる数の組み合わせは

カード1枚のとき　[9]　1通り

カード2枚のとき　([1][8])，([2] [7])，([3] [6])，([4] [[5])　4通り

カード3枚のとき　([1] [2] [6])，([1] [3] [5])，([2] [3] [4])　3通り

以上　1 + 4 + 3 = 8通り

答　　　8通り

東京都市大学付属中学2021年度帰国生算数入試問題1.問7平面図形解説解答

問7　右の図は、1辺が6cmの正方形と、正方形のそれぞれの頂点を中心とした半径6cmの円の円周の1/4を4つ組み合わせたものです。斜線部分の図形のまわり(図の太線部分)の長さの合計は□cmです。

解説解答

中学受験算数等積変形

半径6cm 中心角30°の弧の長さ8個分と6cmの直線2個分の合計が求める長さ

帰国子女入試家庭教師算数

答　　37.12cm

東京都市大学付属中学2021年度帰国生算数入試問題1.問8立体図形の切断解説解答

問8　右の図は、1辺が6cmの立方体です。この立方体を、3点P，Q，Rを通る平面で切り、2つの立体に分けます。このとき、体積の小さいほうの立体の体積は□c㎥です。

解説解答　体積比で求める

3点P，Q，Rを通る平面で切った切り口は下図の通り

それぞれの点をS,T,U,Vとする。

帰国子女オンライン家庭教師

求める立体はPRS-UQVの体積

三角錐T-UQVと三角錐T-RPSの辺の比は　2：6 = 1：3 　なので

三角錐T-UQVの高さと三角錐T-RPSの高さの比も　①：③

③ - ① = ② = 6cmなので　③ = 9cm

三角錐T-UQVと三角錐T-RPSの体積比は　1×1×1：3×3×3 = 1：27

したがって　求める体積は

答　　52c㎥

解説解答　体積比で求める

3点P，Q，Rを通る平面で切った切り口は下図の通り

それぞれの点をS,T,U,Vとする。

中学受験算数立方体の切断

求める立体はPRS-UQVの体積

三角錐T-UQVと三角錐T-RPSの辺の比は　2：6 = 1：3 　なので

三角錐T-UQVの高さと三角錐T-RPSの高さの比も　①：③

③ - ① = ② = 6cmなので　③ = 9cm

三角錐T-UQVは底辺2cm高さ3cm，三角錐T-RPSは底辺6cm高さ9cmなので　求める体積は

切断図形の体積を求める問題

答　　52c㎥　

。