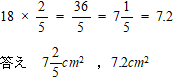東京都市大学中学校帰国生過去問対策
2024年度帰国生入試試験の変更点
A方式[作文型]廃止、 A方式は「国語・算数・英語」3教科入試
帰国生入試A方式「国語」の配点は 50 点
2024年度の東京都市大学中学校帰国生入試は1月6日に実施され、A方式国語型(国語算数英語) B方式2教科型(国語算数) 4教科型(国語算数社会理科)で実施されました。
募集人数は1類Ⅱ類ともに 男子 若干名
帰国生の出願資格は 2011年4月2日から2012年4月1日までに生まれた男子で、①、②の要件を満たすもの。
①日本の義務教育期間における海外就学期間が通算1年以上のもの。
②2024年度入学試験の出願時点で、日本への帰国から3年以内のもの。 ※その他応相談。
2024年度東京都市大学付属中学校帰国生AB方式算数入試問題の出題意図講評は以下の通り
2024 年度 中学入試 帰国生 AB 方式 算数
1.基本的な特殊算や図形の計量の小問集合。四則演算、特殊算の基本問題、規則、図形(平面・立体)の計量を出題した。この問題を通して、種々の問題を速く正確に処理する能力を問うものである。問1・2は計算問題、問3~6は特殊算を幅広い分野から、問7・8は図形の問題を出題した。基本的な計算は例年と変わらない得点率であったが、問6の場合の数に関する問題については、不慣れな問題であったが、想定よりも低い得点率となった。立体図形の計量については、正確に計算する力がやや足りていないように感じた。
2 速さの問題。基本的な問題ではあるが、問題の状況をしっかりと把握し、丁寧に考えていく必要がある。グラフなども活用し、状況を整理することがポイントとなる。問1・2は基本的な問題であり、問題の内容も頻出のタイプであるため、よくできていたと感じる。問3は、走ることと休むことを繰り返す問題のため、状況を整理することが重要で、ダイヤグラムなどを活用し丁寧に解くことが必要であったが得点率は低くなった。
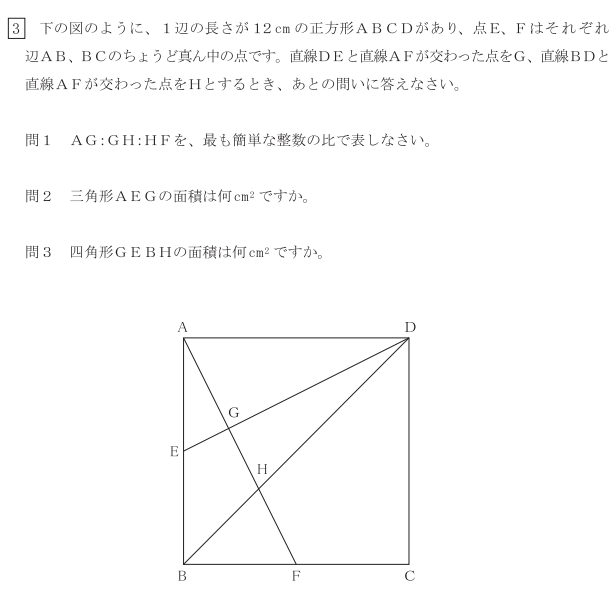
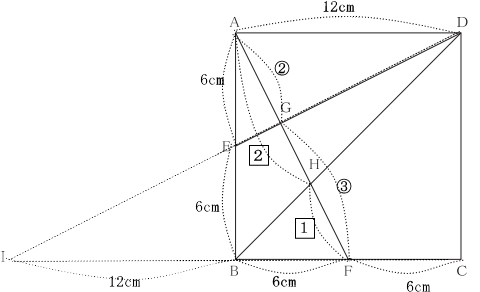
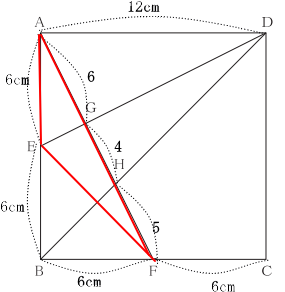
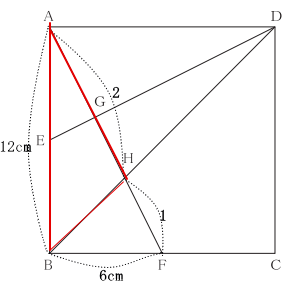
3 本校では特徴的な平面図形と比を絡める問題であり、正方形を題材とした。問1は辺の比、問2・3は面積を求める問題である。辺の比を利用して、面積計算をするという、図形に関する性質を受験生に求めた。本校では頻出となる平面図形と比の問題であったため、よくできていた。合格者平均と受験者平均の差が大きいため、しっかりと練習して確実に得点できることが合否を分ける問題となった様子である。
4 球をやり取りする中で、具体的な実験的操作を通じて、数の規則性を見抜き、的確に計算で処理をすることを問う問題であった。具体的操作を地道に繰り返せることが解決の糸口となる問題であった。球のやり取りが進むにつれて、どのように増減するかを具体的に操作していく中で読み取ることがポイントになる問題であったが、ルールをしっかりと把握できないため、考えが進まないような受験生も多かった様子である。
5.立方体の切断とそれに伴う体積の問題。図形の切断についての基本的な理解が出来ているか。それに伴う体積の計算を正確にできるかを問う問題であった。立方体の切断についての問題。問1の長さを求める問題で難易
度は高くしていないが、想定よりも低い得点率となった。しっかりと問題を把握することができていなかったことに要因があるようである。問2はやや難易度を高く設定した問題であったが、想定よりも得点率は高くなった。