豊島岡女子学園中学校過去問研究
2010年度第1回算数入試問題は 例年通りの問題構成で、1・2 小問集合2問(各4題)、3. 平面図形と場合の数 4.旅人算 5.約束記号の大問5問構成でした。
2010年度第1回算数は 受験者平均点 60.41点 合格者平均点 70.69点 例年通り高得点での合否結果でした。
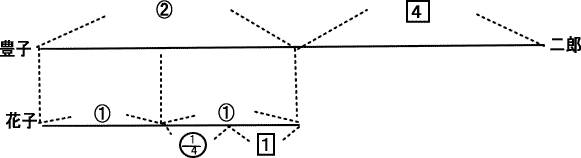
今回は 4 旅人算を解説します。文意の読み取りが重要なポイントです。
算数入試問題 (速さにチャレンジ)
電話: 03-6868-6040
受付時間: 平日 AM 10:00 〜 PM 9:00

超難関中学受験指導はスペースONEのプロ家庭教師にお任せください。

2010年度第1回算数入試問題は 例年通りの問題構成で、1・2 小問集合2問(各4題)、3. 平面図形と場合の数 4.旅人算 5.約束記号の大問5問構成でした。
2010年度第1回算数は 受験者平均点 60.41点 合格者平均点 70.69点 例年通り高得点での合否結果でした。
今回は 4 旅人算を解説します。文意の読み取りが重要なポイントです。
算数入試問題 (速さにチャレンジ)