豊島岡女子学園中学校算数過去問傾向と対策
2013年度第1回算数入試問題は 試験時間50分 配点100点 受験者平均点 59.73点 合格者平均点 72,43点でした。
出題構成は 昨年より1題増え大問6題構成でしたが、出題構成は5までは例年通り、1. 2. 一行問題各4問 3.文章題応用(鶴亀算) 4.規則性 で 5.速さ(平面上の点移動) 6.立体図形の切断 が出題されました。
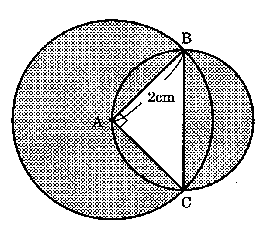
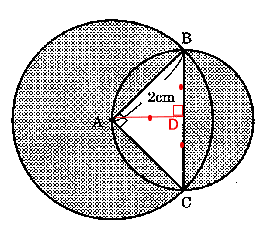
今回は 2.小問集合の中から (4) 平面図形の求積を解説します。円の面積を求める工夫を苦手とする受験生が多い出題の1つです。
算数入試問題 平面図形にチャレンジ