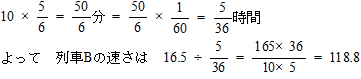早稲田中学校・高等学校過去問対策

大学附属中学受験指導はスペースONEのプロ家庭教師にお任せください。

早稲田中学校合格のための過去問対策

男生徒


早稲田中学校過去問対策


2024年度第１回早稲田中学校入学試験は、応募者855名　受験者740名　合格者253名　入学者226名　国語受験者平均点33.5点　合格者平均点38.9点
算数受験者平均点30.1点　合格者平均点39.8点　理科受験者平均点28.4点　合格者平均点32.1点　社会受験者平均点28.4点　合格者平均点32.1点　総合受験者平均点118.2点　合格者平均点139.8点　合格最低点 129点でした。

2024年度早稲田中学第１回算数入試問題は1.小問集合(1.キセル算　2.割合の文章題　3.場合の数)　2.平面図形3題(1.求角　2.求積　3.容積) 3.通過算　4.推理と論理　5.空間図形の展開図　が出題されました。

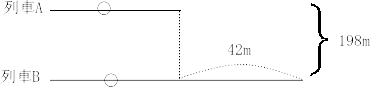
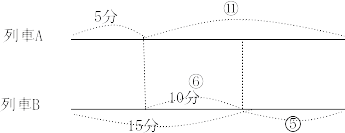
今回は　3.通過算を解説します。

早稲田中学受験指導はスペースONEのプロ家庭教師にお任せください。



早稲田中学校2024年度第１回算数入試問題3.通過算　問題


早稲田中学算数入試問題

早稲田中学校2024年度第１回算数入試問題3.通過算　(1)解説解答

(1)　列車Aが車庫に入るために速度を落として時速21.6kmで走ったとき、停車している列車Bを完全に追い抜くのに33秒かかりました。列車Bの長さは何ｍですか。

解説解答

列車Aが列車Bを完全に追い抜くとき、列車Ａが走る距離は　列車Ａの長さ + 列車Ｂの長さ

時速21,6km = 秒速 21600m÷(60×60) = 6m

列車が追い抜くときの速さは　列車Ａと列車Ｂの速さの差。列車Ｂは停車しているので　速さは秒速6mのまま。

距離 = 速さ×時間なので

列車Aの長さ + 列車Ｂの長さは(距離) =　6×33 = 198m

列車Ａの長さは列車Ｂの長さより42m短いので

分配算より

中学入試問題通過算


(198 + 42) ÷2 = 120


答え　　　120m


早稲田中学校2024年度第１回算数入試問題3.通過算　(2)解説解答

列車Ａと列車ＢはＰ駅からＱ駅まで走ります。342mのトンネルを完全に抜けるのに列車Ａは列車Ｂの2倍の時間がかかります。

(2)　列車Ｂの速度は列車Ａの速度の何倍ですか。

解説解答

列車Bの長さは120mなので、列車Aの長さは120 - 42 = 78m

列車Aと列車Bがトンネルを抜けるときにかかった時間の比は　2：1

列車Aがトンネルを完全に抜けるとき走る距離は　78 + 342 = 420m

列車Aの速さは　440 ÷2 = 210

列車Bがトンネルを完全に抜けるとき走る距離は　120 + 342 = 462m

列車Bの速さは　462÷1 = 462

列車Aと列車Bの速さの比は　210：462 = 5：11

列車Ｂの速度は列車Ａの速度の　　11÷5 = 2.2


答え　　　2.2倍

早稲田中学校2024年度第１回算数入試問題3.通過算　(3)解説解答


　列車Ａと列車ＢはＰ駅からＱ駅まで走ります。342mのトンネルを完全に抜けるのに列車Ａは列車Ｂの2倍の時間がかかります。

(3)　Ｐ駅とＱ駅の間は16.5kmで、途中に5つの駅があります。列車Ａはそれぞれ5つの駅にそれぞれ1分間ずつ停車し、列車Ｂはそれら5つの駅をすべて通過します。Ｐ駅を列車Ａが出発してから15分後に列車Ｂに出発したところ、2つの列車は同時にQ駅に着きました。列車Ｂの速度は時速何kmですか。

解説解答

列車Aは5つの駅にそれぞれ1分ずつ停車し列車Bは列車Aより15分遅れて出発したので　列車Aと列車Bが16.5km走るときの時間の差は　15 - 1×5 = 10分間

列車Aと列車Bの速さの比は　 5：11　距離が等しいので　時間の比は 11：5

線分図より

早稲田中学過去問

⑪ - 5 = ⑥ = 10分

列車Bが16.5kmを走るのにかかった時間⑤は　

早稲田中学過去問解説


答え　　時速118.8km


Copyright(c) 2013 Sample Inc. All Rights Reserved. Design by http://f-tpl.com