山脇学園中学高等学校新着情報
2025年 3月 山脇学園は 専修大学と教育交流提携・関西大学ビジネスデータサイエンス学部と高大連携協定を締結しました。
3月26日、山脇学園中学校・高等学校は、専修大学と教育交流提携に関する協定を締結いたしました。
専修大学は、1880(明治13)年に創立された「専修学校」を前身とする私立大学です。日本で初めて日本語で経済学と法律学を学べる高等教育機関として誕生し、現在は8学部20学科、大学院、法科大学院を擁する人文・社会科学系総合大学へと発展しています。
本校は、神田キャンパスが地理的に近いこともあり、これまでも大学の先生方による出張講義や生徒のキャンパス訪問など、10年以上の長きにわたって交流を重ねて来たことから、このたびの教育交流提携に関する協定締結に至りました。
教育交流提携の内容は下記のとおりです。
⑴ 教育交流プログラムの実施
(例)・大学の先生方による出張講義
・高校生による大学の授業の聴講
・生徒を対象とした司書インターンシップの実施
・生徒による大学図書館の利用
⑵ 教育交流提携校推薦入学試験の実施
⑶ 教育交流提携協議会の開催
⑷ 前3号に掲げるもののほか、中学・高校及び大学が必要と認める事項
今後、本協定に基づく取り組みを通して、大学のご支援をいただきながら、生徒の学びをより一層充実させ、生徒の進路実現に繋げてまいります。
2025年 3月24日プレスリリース
関西大学ビジネスデータサイエンス学部、山脇学園と高大連携協定を締結–DX人材育成に向けた教育支援を開始
高大連携 2025.03.24
関西大学ビジネスデータサイエンス学部、山脇学園と高大連携協定を締結–DX人材育成に向けた教育支援を開始
関西大学が4月に新設するビジネスデータサイエンス学部が、設立前に高大連携協定を結んだ。3月4日、東京都の山脇学園中学校・高等学校と提携し、データサイエンス教育の推進とDX人材の育成を目的とした協力を開始する。新学部が進める高大連携の第一号案件となる。
この協定により、関西大学の教職員が山脇学園を訪れ、生徒向けの講義や説明会を実施。また、大学生と高校生、教職員同士の交流を促進し、DX人材の育成に向けた支援を行う。
山脇学園は1903年創立の伝統校で、「自走力」をテーマに、総合知の一環としてデータサイエンス教育を推進。中等教育段階からDX人材の育成に取り組むべく、今回の提携が実現した。
協定の主な内容は以下の通り。
① 大学教職員による高校生向け講義・説明会の実施
② 大学生と高校生の交流促進
③ 大学・高校教職員間の情報交換
④ 中等教育におけるDX人材育成の協力体制構築
⑤ その他、双方が協議し合意した事項
関西大学商学部でビジネスデータサイエンス学部の学部長に就任予定の鷲尾隆教授は、「生徒たちがデータを通じて社会を洞察し、課題解決に向けた力を養うことを期待している」と述べた。また、山脇学園高等学校の西川史子校長は、「未来社会に向けた最先端の学びを推進する貴学部との連携を大変嬉しく思う」と期待を寄せた。
山脇学園中学校算数過去問研究
20251年度山脇学園中学校国・算1科目入試は、2月1日午後に実施されました。
募集人数50名に対し、志願者数は国語選択550名,数学選択337名、受験者数国語526名,算数319名,合格者数国語167名,算数145名,受験者平均点 国語55.3点,算数58.1点,受験者最高点国語87点,算数95点,合格者平均点国語67.8点,算数72.5点,合格者最低点国語62点,算数62点でした。
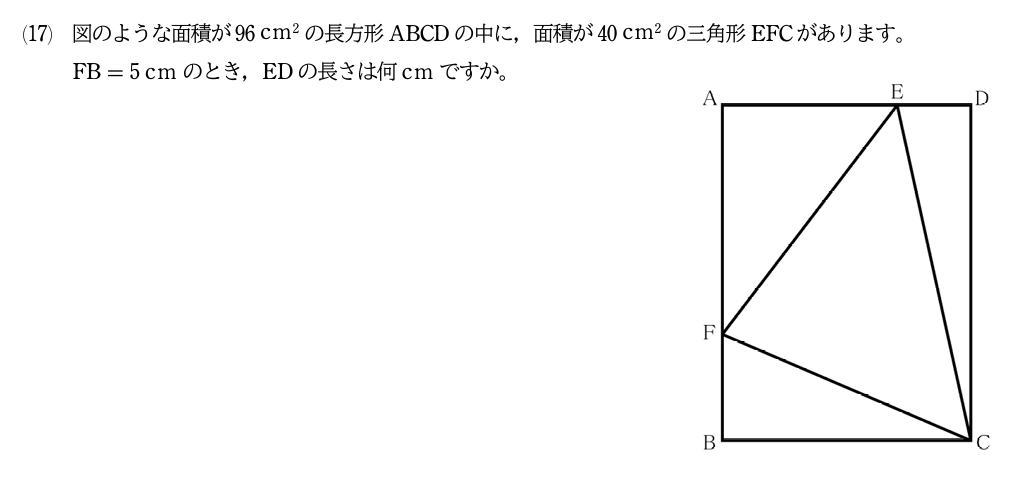
算数入試問題は (1)~(18)枝問なしの1問1答形式,(19) 枝問2問の流水算が出題され (19)のみが途中式を書く解答形式でした。
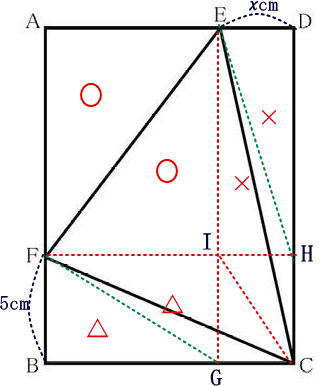
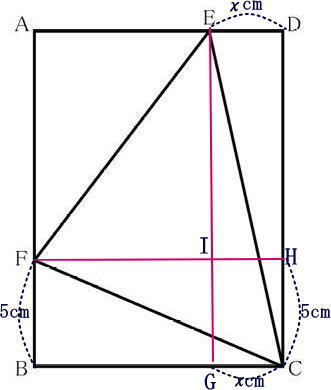
今回は (17) 平面図形を解説します。難問ですが、長方形の中に等積変形を用いて同じ面積の三角形を見つけていくことによって解けます。