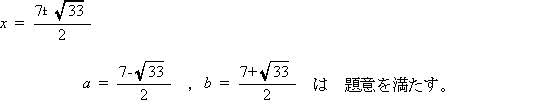中学受験から医学部受験までプロ家庭教師にお任せください。

昭和大学医学部過去問研究2011年度数学入試問題

こんにちは　医学部受験数学・物理・化学指導担当のマス・アーキです。2009年度までは大問４題のうち２題は小問集合でしたが、2011年度１期では 2010年度に続いて大問4題のうち小問集合は１のみ。昨年に続き２．では証明が出題されました。１，３，４は例年通り、結果のみを解答欄に記入する解答形式でした。

昨年に続き英語・数学あわせて試験時間は150分に、数学の問題量は例年と変わりませんが、英語のボリュームが大幅に増えました。数学で時間をなるべく短縮し英語に解答時間をまわす必要があったでしょう。

今回は2　証明について解説します。

（１）　解答

（２）　解答

a3＋b3は整数であり、しかも奇数であることを示せ。 解答 a＋b = 整数 a2- ab ＋b2 = (a2＋b2) - ab 　　　　　　　　　　　= （整数） - （整数）　　（∵　前問(1)より　a2＋b2は整数）　　 　　　　　　　　　　　= （整数）　　　となる。 したがって a3＋b3 = （整数） × （整数） 　　　　　　= 整数となる。　　・・・③ さらに このとき a3＋b3 = (a＋b) - ab (a2- ab＋b2) 　　　　　　= 　（2ｌ + 1) (2k + 1 - 2m) 　　　　　　= 　（2ｌ + 1) ｛2（k - m) +1} k - m= t とおくと 　　　　　　= 　（2ｌ + 1) （2ｔ+1） 　　と書け 　　　　　　=　奇数×奇数 　　　　　　=　奇数　　　　となる。　　　・・・　④ 以上　③，④より a3＋b3は整数であり、しかも奇数である。

（３）　解答

（４）　解答

このような実数a,bで、いずれも整数ではないような例を示せ。 解答 ・　a + b = 7, ab = 4 ・　a,bは２次方程式 ｘ2 - 7x + 4 = 0　の２解となる。（ただしa<b となる。） （∵　（ｘ - a ) (ｘ - b ) = ｘ 2 - ( a + b )ｘ+ ab より） この２次方程式を解くと