青山学院高等部過去問研究
2018年度青山学院高等部一般入学試験数学の出題内容は大問7題構成で1.計算と平面図形，2.確率，3.関数の文章題，4.二次関数のグラフ，5.三角形の辺の比，6.二等辺三角形と直角三角形，7.立体図形が出題されました。
出題内容やボリューム難易度に変更はなく標準レベルの出題でした。
今回は2018年度青山学院高等部一般数学入試問題6.平面図形を解説します。
青山学院高等部 過去問対策
青山学院高等部過去問傾向と対策
高校受験はプロ家庭教師集団スペースONEにお任せください。
青山学院高等部2018年度 数学入試問題 6. 平面図形 問題
青山学院高等部数学入試問題6.平面図形 (1) 解説解答
青山学院高等部数学入試問題6.平面図形 (2) 解説解答
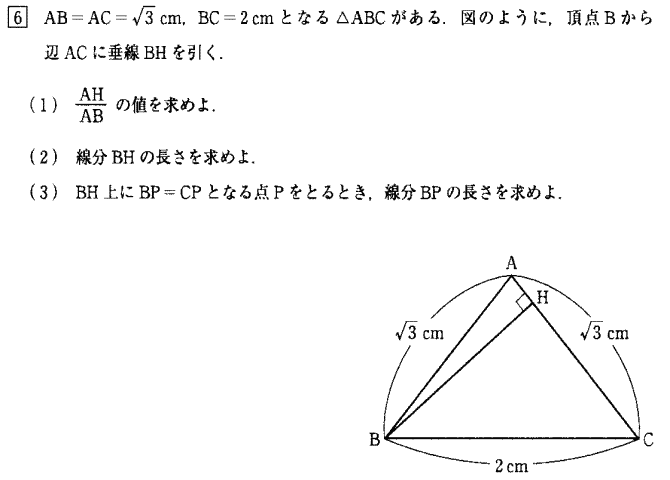
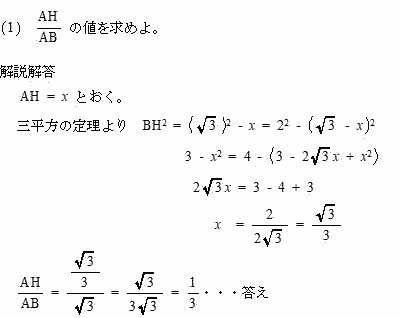
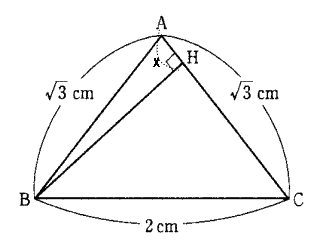
| (2) 線分BHの長さを求めよ。 |
| 解説 |
 |
 |
青山学院高等部数学入試問題6.平面図形(3) 解説解答
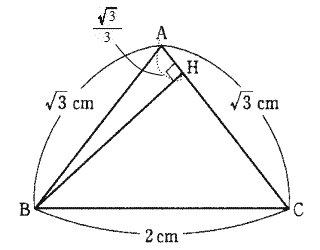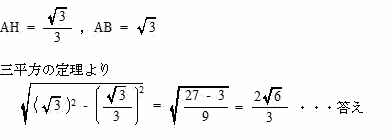| (3) BH上にBP = CPとなる点Pをとるとき、線分BPの長さを求めよ。 |
| 解説 |
 |
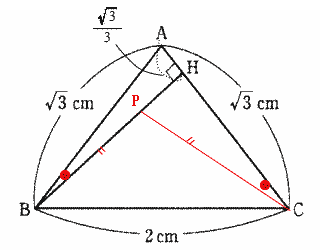| △ABCはAB = CAの二等辺三角形なので底角は等しく ∠ABC = ∠BCA ・・・① △BPCもBP = CPの二等辺三角形なので底角は等しく ∠CBP = ∠BCP・・・② ①，②より ∠ABP = ∠ABC - ∠PBC = ∠PCH = ∠BCH - ∠BCP・・・③ ③と∠BHA = ∠CHP = 90° より 二角相等なので △ABH ∽ △PCH よって AB：BH = PC：CH  |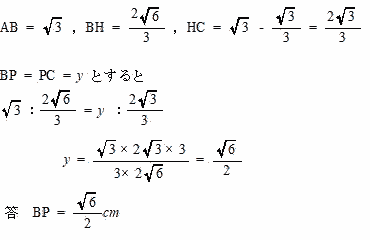
