高校受験はプロにお任せ/プロ家庭教師集団スペースＯＮＥの本郷高校2019年度数学入試問題平面図形

有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。

本郷高校　過去問対策

本郷高等学校数学過去問研究

2019年度本郷高校入試問題は例年通りの出題構成で1.小問集合　5問　2.二次方程式の解　3.　平面図形　4.座標平面　5.三角形に内接する円　6.関数が出題されました。

今回は3.平面図形を解説します。

問題文に図形が描かれていませんので、フリーハンドで図形を描きながら解くと整理がつきます。

本郷高校受験指導はスペースONEのプロ家庭教師にお任せください。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

[3]　本郷高校2019年度　数学入試問題　3.　平面図形　問題

１辺の長さが９の正三角形ＡＢＣがある。辺ＢＣ上にＢＰ＝３となる点Ｐをとり、ＡＰを１辺とする正三角形ＡＰＱをつくる。辺ＡＣとＰＱの交点をＲとするとき、次の問いに答えよ。

⑴　ＡＲの長さを求めよ。

⑵　△ＡＰＱの面積を求めよ。

本郷高校2019年度数学入試問題3.平面図形(1)　解説解答

(!)　ＡＲの長さを求めよ。

解説解答

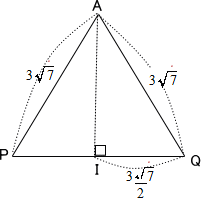
問題文の図形は下図の通り

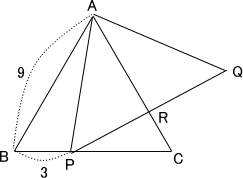
△ABCの頂点Aから底辺BCに垂線を下ろし素の交点をHとする。
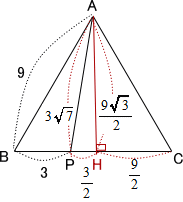
本郷高校数学プロ家庭教師東京

△ABCは正三角形なので　

三平方の定理より　

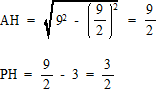
高校受験プロ家庭教師東京

三平方の定理より

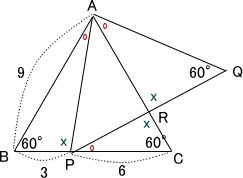
数学専門個別指導プロ

図の通り　△ABP ∽ △PCR

BP = 3 より　PC = 9 - 3 = 6

AB：BP = PC：CR

9：3 = 6：CR 　より　CR = 2

したがって　AR = 9 - 2 = 7・・・答