千葉県立高等学校前期数学過去問研究
2017年度千葉県立高校後期数学入試問題は、１．２．小問集合 ３．関数 ４． 平面図形(証明) ５．座標平面が出題されました。
今回は４． 平面図形(証明)を解説します。
千葉県立高校 過去問対策
有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。
千葉県立高校数学入試問題 2017年度入試問題 4．証明
(1) 解説解答
 |
| 解答 |
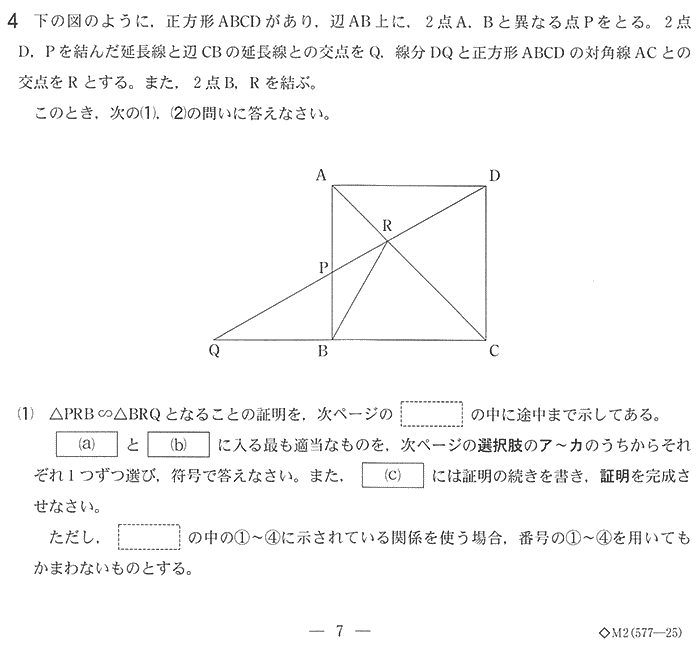
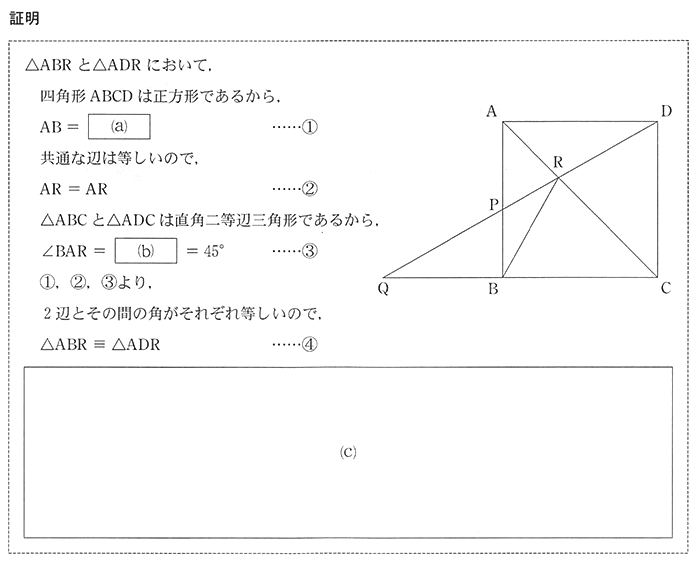
| 途中まで示してある証明は、△ABR≡△ADRを証明することで∠ABR = ∠ADRを証明しているので、続いてAD //QCより平行線の錯角は等しいことから∠ADR = ∠BQRより∠ABR = ∠ADR = ∠BQRを証明することで相似形であることを証明します。 |
| a = AD(イ) b = ∠DAR(オ) |
| 証明 |
 |
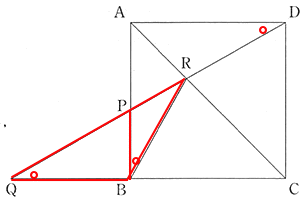| △PRBと△ＢＲＱにおいて、 仮定より AD // QCなので、 ∠ADR = ∠RQB ( 平行線の錯角) (4) より ∠ABR = ∠ADRなので、 ∠ADR = ∠RQB = ∠ABR = ∠RBP より ∠RBP = ∠RQB・・・⑤ ∠PRB = ∠BRQ (共通)・・・⑥ ⑤,⑥より2組の角がそれぞれ等しいので、 △PRB ∽ △ＢＲＱ |
(2) 解説解答
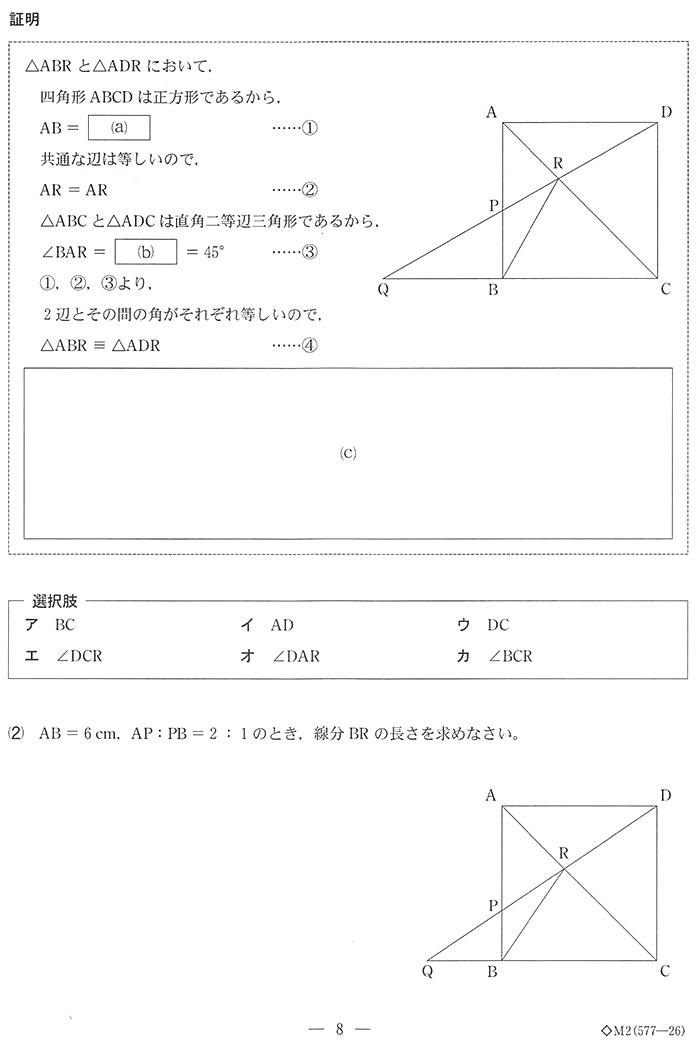
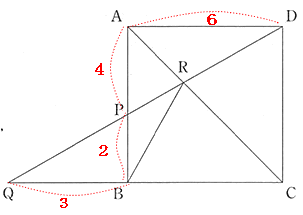
| (2) AB = 6cm, AP：PB = 2：1のとき、線分BRの長さを求めなさい。 |
| 解説 |
 |
 |
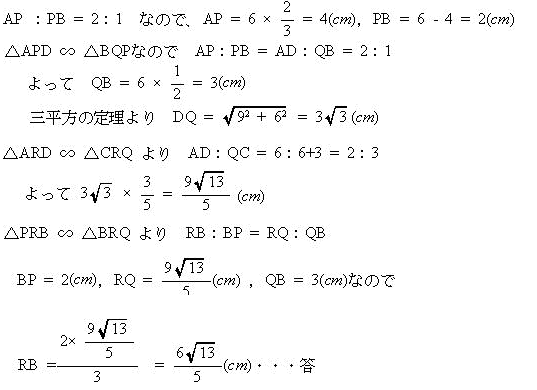