千葉県立高等学校前期数学過去問研究
2018年度千葉県立高校前期数学入試問題から5.規則性を解説します。
青紙の数が奇数列になるっていることに気がつけば簡単に解けます。
千葉県立高校 過去問対策
有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。
千葉県立高校数学入試問題 2018年度入試問題 5．数列
(1) 解説解答
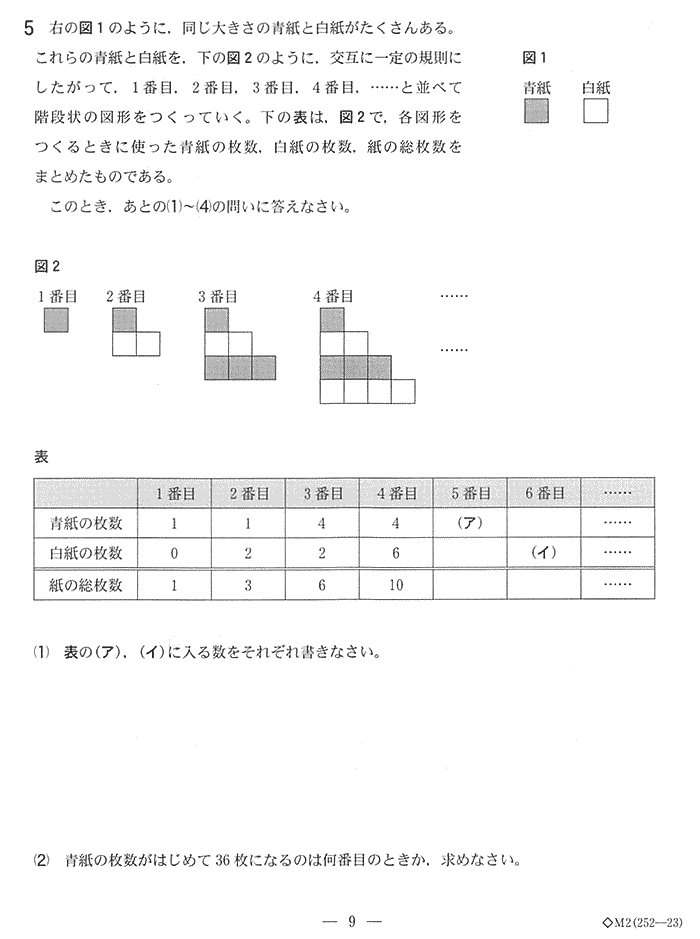
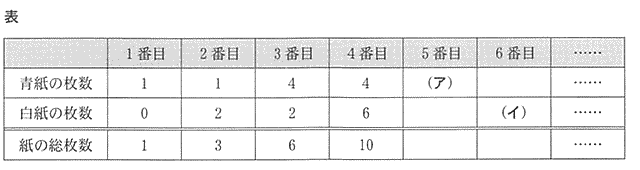
| (1) 表の(ア)，(イ)に入る数をそれぞれ書きなさい。 | |
 |
|
| (ア) 解説解答 | |
| 青紙の枚数は 1番目・2番目 1枚，3番目・4番目 1 + 3 = 4枚・・・ 青紙は奇数番目ごとに 奇数数増えているので 表の5番目は奇数列の3番目になるので、 3×3 = 9枚 |
|
| 答 (ア) 9枚 | |
| (イ) 解説解答 | |
| 白紙の偶数番目の枚数は 2番目2枚 4番目 2 + 4 = 6枚となっているので、表の6番目の白紙の枚数は、偶数列の3番目になるので、 2 + 4 + 6 = 12枚 |
|
| 別解 | |
| 6番目の総枚数は 1 + 2 + ・・・+ 6 = (1 + 6)×6÷2 = 21枚 | |
| 5番目と6番目の青紙の枚数は 9枚なので、 白紙の枚数は 21 - 9 = 12枚 | |
| 答 (イ) 12枚 |
(2) 解説解答
| (2) 青紙の枚数がはじめて36枚になるのは何番目のときか、求めなさい。 |
| 解説 |
| (1) (ア) より青紙は奇数番目ごとに 奇数数増えているので 36 = 6×6 奇数番目の6番目のときはじめて36枚になる。 よって 2×5 + 1 = 11番目 |
| 答 11番目 |
(3) 解説解答
| (3) 30番目のとき、紙の総枚数は何枚になるか、求めなさい。 |
| 解説 |
| 紙の総枚数は 1番目 1枚，2番目 1 + 2 = 3枚，4番目は 1 + 2 + 3 + 4 = (1 + 4)×4÷2 = 10と増えていくので 等差数列の和 より (1 + 30) ×30 ÷2 = 465 |
| 答 465枚 |
(3) 解説解答
| (4) 紙の総枚数が1275枚のとき、白紙の枚数は何枚になるか、求めなさい。 |
| 解説 |
| 等差数列の和より |
 |
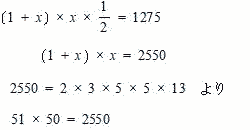| 50番目のとき、紙の総枚数が1275枚になる。 |
| 50番目のとき青紙の枚数は49番目の青紙の枚数と同じになる。49番目は奇数列の (49 + 1)÷2 = 25番目なので、 |
| 50番目のとき青紙の枚数は 25×25 = 625枚 |
| したがって 白紙の枚数は 1275 - 625 = 650枚 |
| 答 650枚 |
