有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。

中央大学附属高校過去問傾向と対策

2012年度中央大学付属高等学校一般入試問題(過去問) 解答解説

中央大学付属高等学校一般入試問題2012年度数学

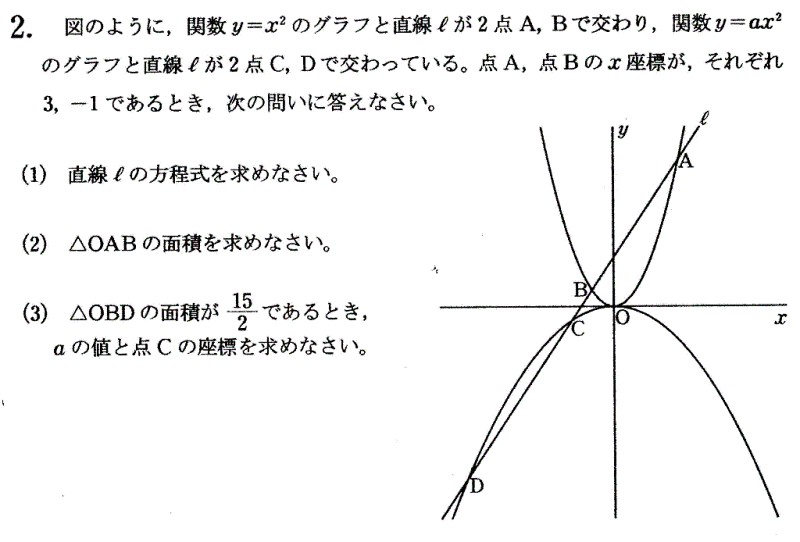
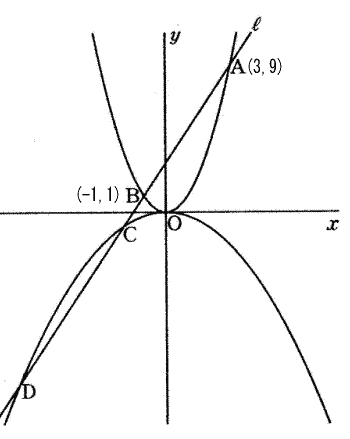
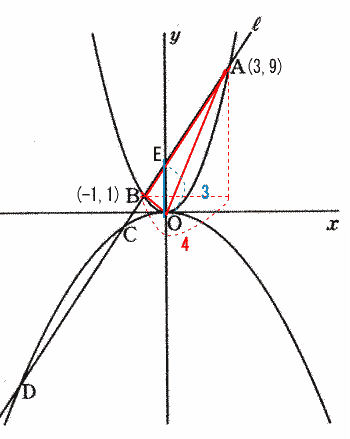
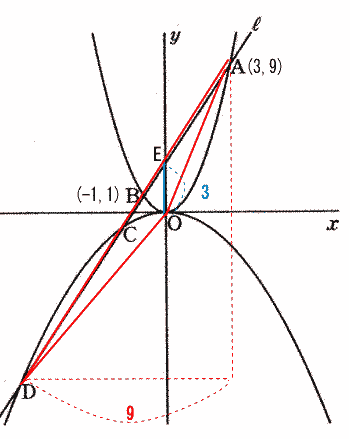
中央大学附属高等学校の2012年度一般入試問題は 1.計算を含む一行問題7問，2.一次・二次関数のグラフ　３．平面図形　辺の比と面積比　４．立体図形の分割と体積　５．数の性質　でした。

解答のみを解答用紙に書く解答形式で、途中式は必要なくまた証明問題もありませんでした。

試験時間は60分、配点は100点でした。


　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

中央大学附属高校2012年度一般数学入試問題2.関数　問題

中央大学附属高校2012年度一般数学入試問題2.関数　問1.解説解答


問1.　直線ｌの方程式を求めなさい。

解説解答



Ａ，Ｂともにｙ＝χ2上の点なので　Aのｙ座標　３2＝９, Bのｙ座標　(-1)2＝１　より　

直線ｌの傾き　(9-1)÷(3--1)＝２

切片　９＝２×３＋ｂ　　ｂ＝３　　
 

答　　　ｙ＝２χ＋３

中央大学附属高校2012年度一般数学入試問題2.関数　問2解説解答




問2.　△ＯＡＢの面積を求めなさい。

解説解答



点Ａ，Ｂのχ座標の差は　３ー（－１）＝４

直線ｌとｙ軸との交点をＥとすると　ＯＥ＝３

よって　△ＯＡＢの面積は　４×３÷２＝６

答　　　　６

中央大学附属高校2012年度一般数学入試問題2.関数　問3.解説解答

問3.　△ＯＢＤの面積が15/2であるとき、aの値と点Ｃの座標を求めなさい。

解説解答




 △ＯＡＢの面積は６なので　△ＯＡＤの面積は　６＋15/2＝27/2

点Ａと点Ｄのχ座標の差は　27/2×２÷３＝９

よって　　点Ｄのχ座標は　３ー９＝ー６

点Ｄは直線ｌ上の点なのでｙ座標は　２×（－６）＋３＝ー９

ｙ＝aχ2の式は　（ー６，－９）を通る放物線なので　

a＝ー9/36＝-1/4

点Ｃの座標は　直線ｌとｙ＝-1/4χ2との交点なので　２χ＋３＝-1/4χ2　を解いて　

χ＝ー２，ー６

点Ｄのχ座標が-6なので、点Ｃのχ座標は-2　ｙ座標は　２(-2)＋３=ー１

答　　　a：　-1/4　　　点Ｃ（-2, -1)




Copyright(c) 2013 Sample Inc. All Rights Reserved. Design by http://f-tpl.com