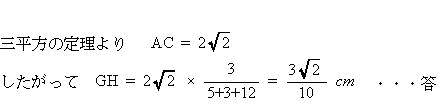江戸川学園取手高校過去問傾向と対策
高校受験はプロ家庭教師集団スペースONEにお任せください。

江戸川学園取手高校　過去問対策

江戸川学園取手高等学校一般入試問題2014年度数学

江戸川学園高等学校の2014年度一般入試問題は例年通り大問4題構成で、出題内容は 1.　小問集合6問，2.　関数，3. 平面図形，4. 立体図形，試験時間は50分、配点は100点でした。

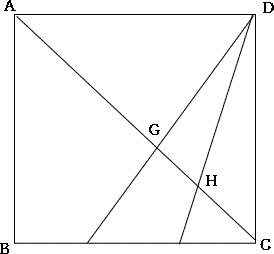
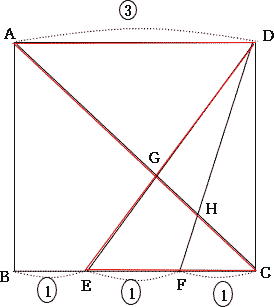
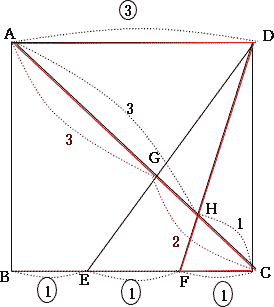
第１回一般入試算数入試結果は　医科コース　受験者平均点87.8点，合格者平均点93.5点，受験者最高点　100点，普通科コース　受験者平均点83.4点，合格者平均点86.2点，受験者最高点　100点でした。難問はなく、特に大問は誘導に従って題意をくみ取って解いていく練習をしましょう。今回は　３．平面図形を解説します。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

江戸川学園取手高校　2014年度　数学入試問題　3.平面図形　問題

図のように1辺の長さが2cmの正方形ABCDがあります。辺BCを3等分する点を、B側から順にE，Fとし、線分ACと線分DE，DFとの交点をそれぞれG，Hとします。このとき、次の問いに答えなさい。



(1)　EG：GDの比を、もっとも簡単な整数の比で表しなさい。

(2)　線分GHの長さを求めなさい。

(3)　四角形EFHGの面積を求めなさい。

江戸川学園取手高校　2014年度　数学入試問題　3.平面図形　解説解答

(1)　EG：GDの比を、もっとも簡単な整数の比で表しなさい。

解説




△ECGと△DAGにおいて　∠ECG = ∠DAG (平行線の錯角)

∠CGE = ∠AGD (対頂角)　二角相等より△ECG∽△DAG

したがって　EC ：DA = EG：GD = 2：3

答　　EG：GD = 2：3

(2)　線分GHの長さを求めなさい。

解説


(1)　より　EG：GD = CG：GA = ②：③

また△ECHと△DAHにおいて　∠FCH = ∠DAH (平行線の錯角)

∠CHF = ∠AHD (対頂角)　二角相等より△ECH∽△DAH

したがって　EC ：DA = CH：HQA = [1]：[3]

CH + HA = CG + GA = CA

② + ③ = [1] + [3]

CAの長さを5と4の最小公倍数20とすると、

CH : HA = 5：15 ,CG : GA = 8：12　より　CH：HG：GA = 5：3：12


(3)　四角形EFHGの面積を求めなさい。

解説







Copyright(c) 2013 Sample Inc. All Rights Reserved. Design by http://f-tpl.com