城北高等学校過去問研究
2017年度城北高等学校数学入試問題は昨年同様大問5題構成でした。[1]の小問集合4問,[2]の平面図形に関する問題3問。[3]規則性 [4]関数のグラフ [5]球に関する問題が出題されました。
今回は3.平面図形に関する問題3問を解説します。図形の性質を理解して解きましょう。
城北高校過去問解説解答
城北高校過去問傾向と対策
高校受験はプロ家庭教師集団スペースONEにお任せください。
城北高校2017年度数学入試問題2.平面図形 問題
城北高校2017年度数学入試問題2.平面図形 (1) 解説解答
|
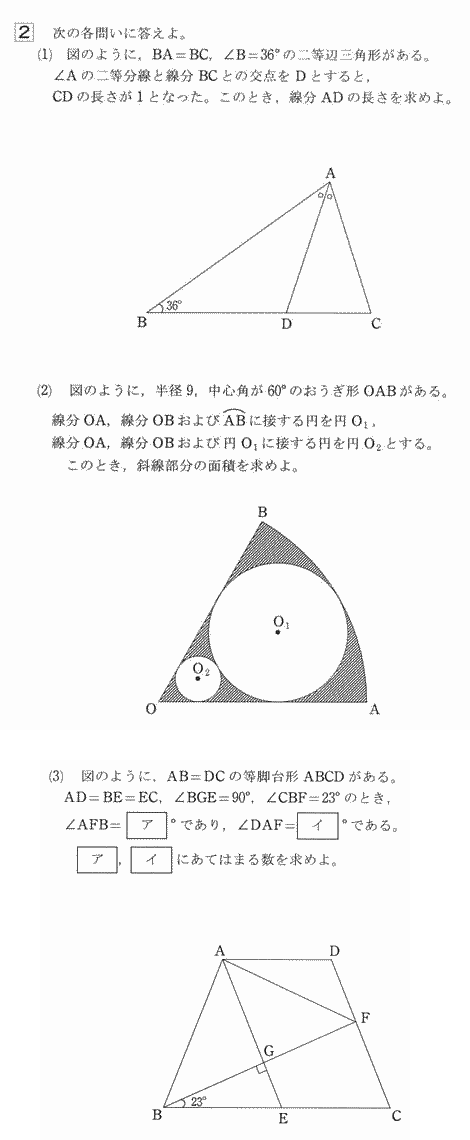
(1) 図のように、BA=BC，∠B = 36°の二等辺三角形がある。∠Aの二等分線と線分BCとの交点をDとすると、CDの長さが1となった。このとき、線分ADの長さを求めよ。
|
| 解説 |
 |
城北高校2017年度数学入試問題2.平面図形 (2) 解説解答
城北高校2017年度数学入試問題2.平面図形 (3) 解説解答
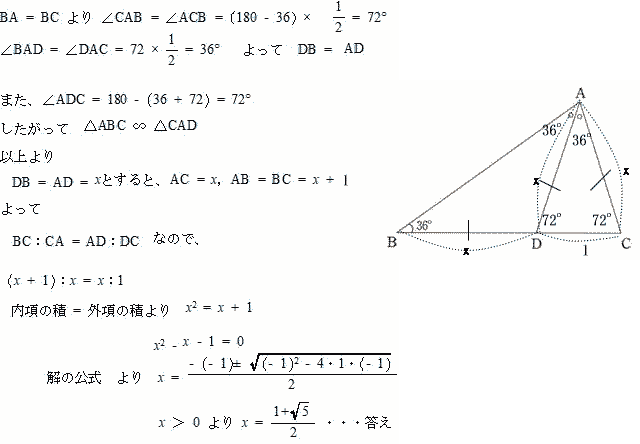| (3) 図のように、AB = DCの等脚台形ABCDがある。AD = BE = EC，∠BGE = 90°，∠CBF = 23°のとき、∠AFB = [ア]°であり、∠DAF = [イ]°である。 |
| [ア]解説解答 |
 |
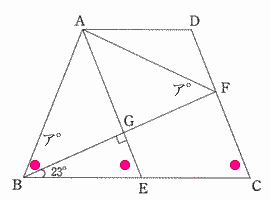| 四角形ABCDは等脚台形であり、AD//BE//BCなので、△ABEは二等辺三角形，四角形AECDは平行四辺形。 また、二等辺三角形の頂角に二等分線は底辺を直交するので、△ABFは二等辺三角形。 よって∠ABG = ∠AFB = ア° したがって ∠ABE = ∠AEB = 90°- 23°= 67°なので、 ∠ABG = 67°- 23°= 44° |
| 答え 44° |
| [イ]°解説解答 |
| |
| 平行四辺形の向かい合う角は等しいので、∠ECD = ∠DAE = 67° ∠FAG = 90°- ∠GFA = 90°- 44°＝ 46° ∠DAF = ∠DAE - ∠FAE = 67°- 46°= 21° |
| 答え 21° |
