開成高等学校数学過去問研究
開成高等学校2020年度数学入試問題は例年通り大問4題構成。1.小問2問， 2.座標平面 3.場合の数 4.立体図形立体上の点移動が出題され、空間図形が多く出題されました。今年度は2.で証明問題が出されました。
今回は、2.座標平面問題を解説します。外接円の中心や接点など、平面図形に対する応用力を求められる出題でした。
数学入試問題
開成高校過去問解説解答
開成高校過去問傾向と対策
高校受験はプロ家庭教師集団スペースONEにお任せください。
開成高校2020年度数学入試問題2．座標平面 問題
開成高校2020年度数学入試問題2．座標平面 (1) 解説解答
(1) 3点A，B，Cそれぞれの座標を求めよ。
解説解答
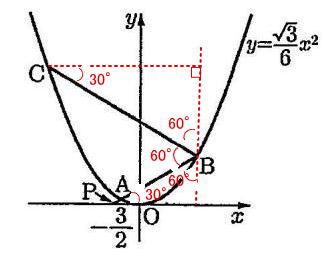
∠OPA = ∠OPB = 30°なので、内角の大きさがそれぞれ30°，60°の直角三角形の辺の比より 直線PBの傾きは
開成高校2020年度数学入試問題2．座標平面 (2)解説解答
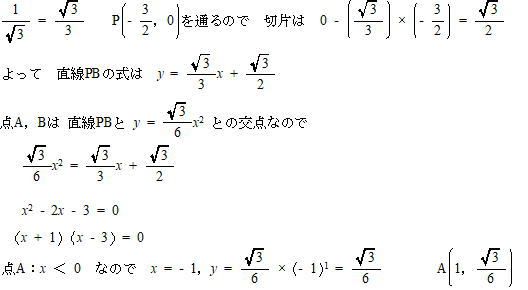
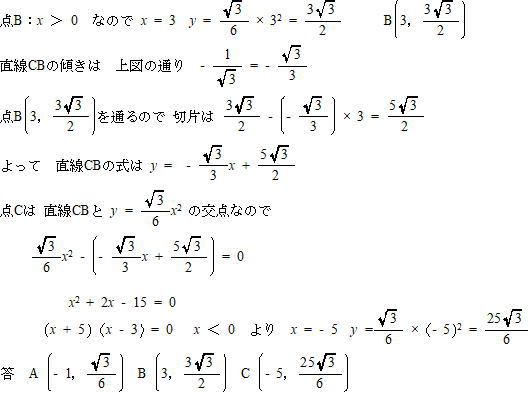
(2) 3点A，B，Cを通る円の中心の座標を求めよ。
解説解答
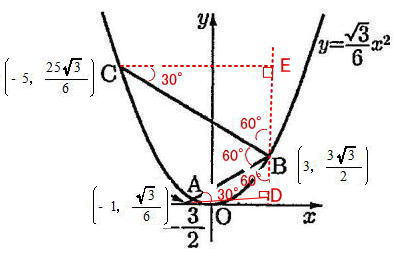
図のように 点Bからy軸に平行な直線を，点Aからx軸に平行な直線を引き、その交点をDとする。
点Bからy軸に平行な直線と点Cからx軸に平行な直線との交点をEとする。
△ADB∽△CEBなので
よって AB：BC = 1：2 また∠ABC = 60°なので△ABCは∠CABの直角三角形
したがって △ABCは∠CAB = 90°の三角形なので 3点A，B，Cを通る円の中心はCBの中点になる。
CBの中点の座標は
開成高校2020年度数学入試問題2．座標平面 (3) 解説解答
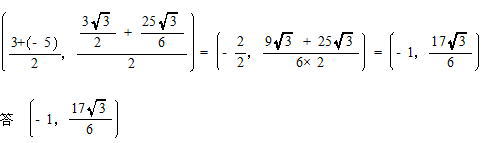
(3) 点Bを接点とする(2)の円の接線の式を求めよ。
解説解答
円の接線は接点で半径と垂直に交わる。円の半径は直線CB上にあるので直線CBの傾きと接線の傾きの積は - 1となる。
開成高校2020年度数学入試問題2．座標平面 (4)解説解答
