京華女子高校2021年度一般数学入試問題
2021年度京華女子高校一般第１回数学入試問題は1.四則計算4問 2.小問集合7問 3.関数 4.場合の数 5.平面図形(相似形)が出題されました。例年通りの出題内容で基本～応用レベルの難易度になります。
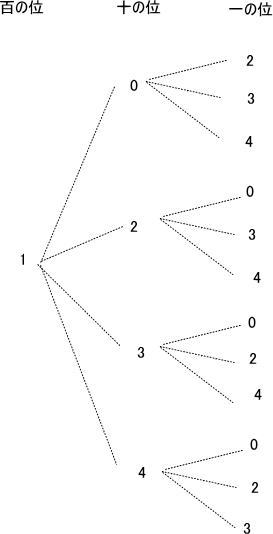
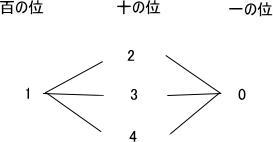
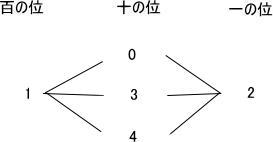
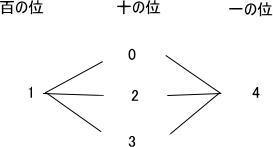
今回は4.場合の数を解説します。高校受験数学入試問題として基本的な知識を復習することのできます。確実に正答しましょう。
京華女子高校過去問傾向と対策
京華女子高校入試問題の傾向と対策
高校受験はプロ家庭教師集団スペースONEにお任せください。
京華女子高校2021年度数学入試問題4.場合の数 問題
(1) 3桁の整数は全部で何通りできるか。
(2) (1)のうち偶数は何通りできるか。
(3) (1)のうち3の倍数は何通りできるか。
京華高校2021年度数学入試問題4.場合の数 (1) 解説解答
解説解答
百の位の数は 1，2，3，4 の4通り
十の位の数は 百の位の数を除き、0が加わるので 4通り
一の位の数は 十の位の数を除いて 3通り
積の公式より 4×4×3 = 48
答 48通り
別解
樹形図の通り, 百の位の数が1のとき 4×3 = 12通り
同様に百の位が2，3，4のときもそれぞれ12通りあるので、12×4 = 48
答 48通り
京華女子高校2021年度数学入試問題4.場合の数 (2)解説解答
(2) (1)のうち偶数は何通りできるか。
解説解答
偶数になるのは、一の位が0.2.4になるとき
一の位が0のとき 百の位は 1,2,3,4の場合
十の位は 百の位の数を除いて 3通り
よって 一の位が0のとき 積の公式 より 4×3 = 12通り
一の位が 2のとき 百の位は 0,2を除いて 1,3,4の3通り
十の位は 0,1,3,4のうち 百の位の数を除いて 3通り
よって 一の位が2のとき 積の公式 より 3×3 = 9通り
一の位が 4のときは 一の位が2のときと同様に 9通りとなる。
したがって 偶数は 12 + 9 + 9 = 30通り
答 30通り
別解
樹形図の通り, 一の位が0，百の位が 1の場合 3通り。同様に 百の位は2,3,4の場合も 3通りずつなので
一の位が0のとき 3×4 = 12通り
樹形図の通り, 一の位が2，百の位が 1の場合 3通り。同様に 百の位は3,4の場合も 3通りずつなので
一の位が0のとき 3×3 = 9通り
樹形図の通り, 一の位が4，百の位が 1の場合 3通り。同様に 百の位は2,3の場合も 3通りずつなので
一の位が4のとき 3×3 = 9通り
以上から 12 + 9×2 = 30
答 30通り
京華女子高校2021年度数学入試問題4.場合の数(3)解説解答
解説解答
3の倍数になるのは、3桁の整数の各位の和が3の倍数となるとき。
3つの整数の和が3の倍数となる組み合わせは (0，1，2) (0，2，4) (1，2，3) (2，3，4)
(0，1，2)の場合3桁の整数は 102，120，201，210 の4通り
(0，2，4)の場合も同様に4通り
(1，2，3)の場合3桁の整数は 123，132，213，231，321，312 の6通り
(2，3，4)の場合も同様に6通り
よって 3の倍数の個数は 4×2 + 6×2 = 20通り
答 20通り
