慶應義塾女子高校過去問傾向と対策
高校受験はプロ家庭教師集団スペースONEにお任せください。
慶応義塾女子高校 過去問対策

慶應義塾女子高等学校数学過去問研究
慶応義塾女子高等学校は 一般入試・帰国生入試とも同一問題です。
2021年度慶応義塾女子高等学校一般入学試験は、募集人数約80名 志願者数454名 受験者数438名 合格者数130名 補欠合格者数26名 補欠入学許可数0名 入学者数76名
帰国入学試験は、募集人数若干名 志願者数58名 受験者数56名 合格者数23名 補欠合格者数5名 補欠入学許可数0名 入学者数20名でした。
数学入試問題は独立小問が無くなり 大問5題構成で 1.連立方程式の応用 2.関数のグラフ 3.空間図形 4.平面図形(円の性質と相似形) 5.二次方程式の応用と確率が出題されました。例年通り証明問題はなく、作図も出題されませんでした。
今回は4.平面図形(円の性質と相似形)を解説します。
慶応義塾女子高校2021年度数学入試問題4.平面図形(円の性質と相似形)(1)解説解答
[1] ∠BDPと∠DPEの大きさを求めなさい。
解説解答

∠BDPは 直径BPの円周角なので90°
∠ABC = ∠DBE
弧DEの円周角なので ∠DBE = ∠DPE = 30°
答 ∠BDP = 90°,∠DPE = 30°
[5] 線分AP,線分AFの長さをそれぞれ求めなさい。
線分APの長さ 解説解答

∠PDF = ∠PAFなので、4点P,D,A,Fは同一円周上にある点である。
また ∠PDB = 90°なので ∠ADP = 90°。円周角の定理の逆よりAPは4点PDAFを通る円の直径である。
△ADPにおいて、∠ADP = 90°,∠PAD = 45° よって ∠DPA = 45° なので △ADPは直角二等辺三角形
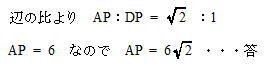
線分AFの長さ 解説解答

△BPEと△APFにおいて
∠EBP = ∠FAP・・・①
∠PEB = 90°(直径BPの円周角),∠PFA = 90°(直径APの円周角) よって ∠PEB = ∠PFA・・・②
①,②より △BPE ∽ △APF
したがって BP:AP = BE:AF